Метод определения устойчивости откоса круглоцилиндрический

Оценка устойчивости откосов и склонов методом круглоцилиндрических поверхностей скольжения

Метод круглоцилиндрических поверхностей скольжения широко применяется на практике.

Сущность метода круглоцилиндрических поверхностей скольже­ния сводится к следующему. Предположим, что грунтовый массив смещается по круглоцилиндрической поверхности АС с центром в точке О (рис. 19). Условием равновесия призмы обрушения будет: сумма моментов всех сил относительно точки вращения 0 равна нулю, т.е. . Для составления уравнения моментов относительно точки вращения 0 разобьем призму скольжения АВС вертикальными сече­ниями на ряд отсеков. 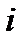Разбивка призмы обрушения на отсеки произ­водится с учетом неоднородности грунта призмы и профиля склона так, чтобы в пределах отрезка дуги скольжения основания каждого -го отсека прочностные характеристики и были бы постоянными.

Силой, действующей на каждый отсек, будет его вес .

Принимаем условно за точку приложения веса каждого отсека точку пересечения отвесной линии (вес отсека) с серединой отрезка соответствующей дуги скольжения.

Разложим вес отсека Q_i на нормальную N_i (по направлению ра­диуса вращения) (N_i и касательную T_i (по направлению, перпендику­лярному радиусу) составляющие к дуге скольжения в точке их прило­жения.

(57)

Момент сил, сдвигающих отсек относительно точек вращения О, определится по формуле

(58)

где — число отсеков в призме обрушения.

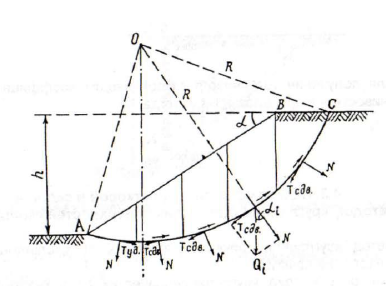
Рис. 19. Схема к расчету устойчивости откосов

методом круглоцилиндрических поверхностей скольжения

Удерживающие силы в пределах основания каждого отсека бу­дут обусловлены сопротивлением сдвигу за счет сил внутреннего тре­ния, пропорциональных нормальной составляющей , и сцепления грунта по поверхности скольжения:

(59)

где l_i — длина дуги основания i -того отсека;

φ_i — угол внутреннего трения;

c_i — сцепление грунта.

Момент сил, удерживающих призму скольжения, определится по формуле

(60)

Коэффициент устойчивости η откоса будет равен отношению мо­мента сил, удерживающих призму скольжения, к моменту сил сдви­гающих:

(61)

Однако уравнение (61) не дает однозначного ответа на постав­ленный вопрос, так как можно провести множество круглоцилинд­рических поверхностей с центром в точке О. Необходимо из всех воз­можных дуг поверхностей скольжения выбрать наиболее опасную. Для решения этой задачи с достаточным приближением применяют следующий прием.

Из верхней грани откоса проводят наклонную линию (вверх) под углом 36° к горизонту (рис. 20). На этой линии намечают точки и т.д. — центры дуг поверхностей скольжения — по следующему принципу. Точка находится на расстоянии (0,25 + 0,4m)h, где ; h — высота откоса. Остальные центры последовательно от­мечают на расстоянии 0,3h от предыдущего.

Рис. 20. Определение центра вращения наиболее опасной

Удерживающие силы в пределах основания каждого отсека бу­дут обусловлены сопротивлением сдвигу за счет сил внутреннего тре­ния, пропорциональных нормальной составляющей , и сцепления грунта по поверхности скольжения:

(59)

Для каждой дуги поверхности скольжения, проведенной из цен­тров и т.д., определяют коэффициенты устойчивости по фор­муле (61). Минимальное значение коэффициента устойчивости определит положение наиболее опасной поверхности скольжения.

Как указывает Н.А. Цытович, некоторые усовершенствования и упрощения расчетов ‘по методу круглоцилиндрических поверхностей скольжения внесены Г.И. Тер-Степаняном и М.Н. Гольдштейном.

Коэффициент устойчивости в этом случае вычисляют по формуле

(62)

где А и В — коэффициенты, зависящие от геометрических размеров сползающей призмы, выраженные в долях от высоты откоса h.

f=tgφ — коэффициент внутреннего трения.

Значения этих коэффициентов и приведены в табл. 8.

Величина h, вычисляемая из выражения (62), будет иметь вид

(63)

По формулам (62) и (63) и данным табл. 8 можно легко вычислить значения коэффициентов устойчивости откоса и предельную высоту откоса h при принятой устойчивости.

Значение коэффициентов А и В для приближенного расчета

Устойчивости откосов

Заложе-ние откоса 1:m	Поверхность скольжения проходит через нижнюю кромку откоса	Поверхность скольжения проходит через основание и имеет горизонтальную касательную на глубине
A	B	A	B	A	B	A	B	A	B
1: 1,00	2,34	5,79	2,56	6,1	3,17	5,92	4,32	5,8	5,78	5,75
1: 1,25	2,64	6,05	2,66	6,32	3,24	6,62	4,43	5,86	5,86	5,8
1: 1,50	2,64	6,5	2,8	6,53	3,32	6,13	4,54	5,93	5,94	5,85
1: 1,75	2,87	6,58	2,93	6,72	3,41	6,26	4,65	6,02	5,9
1: 2,00	3,23	6,7	3,1	6,87	3,53	6,4	4,78	6,08	6,1	5,95
1: 2,25	3,19	7,27	3,26	7,23	3,66	6,56	4,9	6,16	6,18	5,98
1: 2,50	3,53	7,3	3,46	7,62	3,82	6,74	5,08	6,26	6,26	6,02
1: 2,75	3,59	8,02	3,68	4,02	6,95	5,17	6,36	6,34	6,05
1: 3,00	3,59	8,91	3,93	8,4	4,24	7,2	5,31	6,47	6,44	6,09

Пример. Определить предельную высоту откоса с уклоном 1:2, если , 22°, =12 кПа, =18 кН/м 3 . Поверхность скольжения про­ходит через нижнюю кромку откоса. Значения коэффициентов А и В находим по табл. 8. Подставив их в формулу (63), будем иметь

(м)

Задача № 4. Оценка степени устойчивости откоса методом круглоцилиндрических поверхностей скольжения (КЦПС)

Анализ устойчивости массивов грунта имеет большое практическое значение при проектировании земляных сооружений: насыпей, выемок, дамб; при оценке устойчивости естественных склонов.

Устойчивость откосов зависит от:

— прочности грунтов, слагающий откос и в его основании (параметров сопротивления грунтов сдвигу φ; с);

— нагрузок на поверхности откоса;

— фильтрация воды через откос.

Главнейшие причины нарушения устойчивости земляных масс: 1 – эрозионные процессы; 2 – нарушение равновесия.

Эрозионные процессы протекают весьма медленно и обычно не рассматриваются в механике грунтов.

Нарушение равновесия массивов грунта может происходить внезапно, со сползанием значительных масс грунта – такие нарушения равновесия называются оползнями. Этот вид нарушений равновесия является наиболее частым.

Возможными причинами нарушения устойчивости откосов являются:

— излишняя его крутизна;

— подрезка откоса в нижней части;

— утяжеление откоса вследствие увлажнения грунта;

— уменьшение параметров сопротивления сдвигу грунта тела откоса вследствие увлажнения, промерзания и оттаивания и других факторов;

— нагрузка на гребень откоса;

Метод круглоцилиндрических поверхностей скольжения широко применяется на практике для оценки устойчивости откосов насыпей и естественных склонов и является наиболее распространенным из методов расчета. Метод основывается на опытных данных о форме поверхностей скольжения при оползнях вращения, при этом самое невыгодное их положение определяется расчетом.

Задача расчета заключается в определении коэффициента устойчивости природного склона или откоса насыпи для наиболее опасной поверхности скольжения.

При крутизне откоса больше предельной происходит обрушение его части по поверхности, которую без большой погрешности можно принять за круглоцилиндрическую с радиусом R (рис.4.1).

Считая задачу плоской, толщина расчетного откоса по направлению его протяженности принимается 1 м. На плоскости чертежа след поверхности скольжения имеет вид части окружности радиуса R с центром в точке О.

Степень устойчивости откоса оценивается по величине коэффициента, представляющего собой отношение суммы моментов сил (относительно центра в точке О), удерживающих призму обрушения в устойчивом состоянии – М_уд, к сумме моментов сил, вызывающих потерю устойчивости призмы обрушения – М_вр:

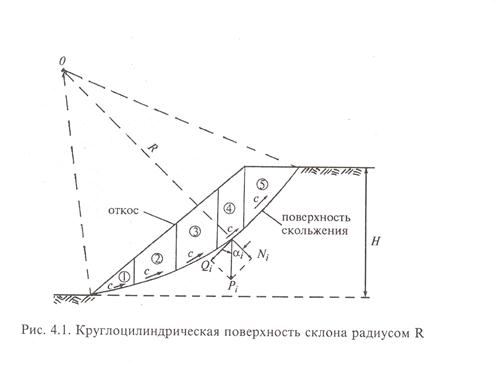
Для обеспечения устойчивости склона или откоса необходимо, чтобы коэффициент запаса устойчивости К_зап был больше 1.

В зависимости от класса ответственности сооружения требуемая величина коэффициента запаса устойчивости К_зап=1,25 – 1,80 и регламентируется соответствующими типу и классу сооружения нормами (СНиП).

Решение задачи осложняется неопределенностью положения центра вращения О_мин для которого значение коэффициента запаса К_зап будет иметь минимальное значение из всех возможных значений.

Для облегчения определения расположения центра О_мин предложен ряд приемов. Наименее трудоемким для однородных откосов является способ определения координат положения центра О_мин по графику норвежского ученого Ямбу (рис. 4.2).

В данном способе по углу наклона откосной линии к горизонту β и обобщенному показателю λ=γ₁Htgφ/c

Определяют относительные координаты х_о и у_о центра вращения Омин. Абсолютные координаты центра вращения при этом равны:

Точку начала координат помещают в точку пересечения линии откоса с горизонтальной линией основания. Ось абсцисс (ось х) с положительными значениями х направляют вправо о начала координат, ось ординат (ось у) – вертикально вверх.

Радиус R поверхности скольжения определяется по расстоянию от центра вращения О_мин до точки пересечения нижнего горизонта откоса и откосной линии (начала координат) (рис.4.2).

Радиусом R из точки О проводят в пределах тела откоса часть круглоцилиндрической поверхности скольжения, определяющей очертание потенциально опасной призмы обрушения.

Для определения коэффициента запаса устойчивости призма обрушения разбивается на ряд блоков с соблюдением ряда правил:

— поверхность скольжения в пределах одного блока должна находиться в грунте одного типа и состояния;

— вертикальные границы между смежными блоками должны проходить через точки перелома очертания откосной линии (если поверхность откоса имеет сложное очертание);

— целесообразно при разбивке призмы обрушения на расчетные блоки ширину блоков принимать одинаковой.

Вес каждого блока Р_i определяют как:

где γ_l — удельный вес грунта в пределах блока, кН/м 3 ;

S_i — площадь i-го блока, определяется как площадь трапеции или треугольника, м 2 ; 1 – толщина i-го блока, равна 1,0 м.

Вес каждого блока Р_i раскладывается на нормальную N_i и касательную Q_i составляющие, приложенные в точке пересечения линии действия силы тяжести с поверхностью скольжения:

где α_i — угол между направлением нормали к поверхности скольжения i-го блока (в точке пересечения линии действия силы тяжести и поверхности скольжения) и линией действия силы тяжести (веса) i-го блока.

Сила сопротивления сдвигу по поверхности скольжения в пределах i-го блока, обусловленная внутренним трением, определяется по формуле:

Сила сопротивления сдвигу по поверхности скольжения в пределах блока, обусловленная действием сцепления с грунта:

Где l_i — длина дуги поверхности скольжения в пределах расчетного блока (принимается по хорде).

К_зап= ΣМ_уд / ΣМ_вр= или сокращая на R:

К_зап=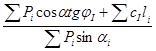

При откосе сложенном однородным грунтом:

где L – длина дуги поверхности скольжения, м

Для конкретного варианта строится в масштабе откос, определяется точка О по графику (рис.4.2), строится поверхность скольжения, оползневое тело разбивается минимум на 5 расчетных блоков, определяется N_i и Q_i для каждого блока и коэффициент запаса устойчивости.

ПРИМЕР РАСЧЕТА. Исходные данные: высота Н=12 м; склон сложен суглинком с параметрами: γ=19,9 кН/м 3 ; φ=20,5 0 ; с=40 кПа; крутизна склона характеризуется углом наклона линии склона к горизонту β=40 0 .

Требуется: оценить устойчивость склона.

Расчетная схема склона показана на рис. 4.3.

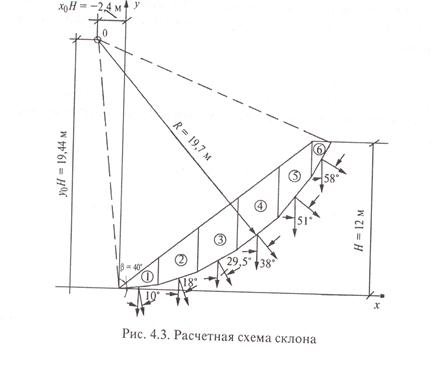
ПОСЛЕДОВАТЕЛЬНОСТЬ РАСЧЕТА

По графику Ямбу (рис. 4.2) определяются координаты центра тяжести вращения О:

Радиусом R=20,6 м из центра О проводится поверхность скольжения (рис. 4.3). Радиус R поверхности скольжения определяется по расстоянию от центра вращения О до точки пересечения нижнего горизонта откоса и откосной линии.

Оползневое тело (призма обрушения) разбивается на ряд блоков (не менее 5-ти).

Определяется длина поверхности скольжения в пределах каждого блока l_i угол α_i (по тангенсу угла наклона), а также P_i; N_i; Q_i:

м	кН	кН	кН
l1=3	α1=10 0	P1=19,9´(3,0 +1,4)/2=53,7	N1=53,7´0,98=52,6	Q1=53,7´0,17=9,1;
l2=3,2	α2=18 0	P2=19,9´3(1,8+3,3)/2=152,2	N2=152,2´0,95=144,6	Q2=152,2´0,31=47,2;
l3=3,3	α3=29,5 0	P3=19,9´3(3,3·4,0)/2=217,9	N 3=217,9´0,87=189,6	Q3=217,9´0,49=106,8;
l4=3,8	α4=38 0	P4=19,9´3(4+4,2)/2=244,8	N 4=244,8´0,79=193,4	Q4=244,8´0,62=151,8;
l5=3,4	α5=51 0	P5=19,9´2,3(4,2+3,6)/2=178,5	N 5=178,5´0,63=112,4	Q5=178,5´0,78=139,2;
l6=4,0	α6=58 0	P6=19,9 ´ (2+3,6)/2=71,6	N 6=71,6´0,53=37,9	Q6=71,6´0,85=60,9.

К_зап=

Из расчета следует, что откос находится в устойчивом состоянии и характеризуется минимальным коэффициентом запаса К_зап=2,1.

Варианты расчетного задания № 4

Оценить степень устойчивости склонов и откосов методом кругло-цилиндрической поверхности скольжения (КЦПС).

Номер варианта задания определяется по сумме трех последних цифр шифра студента.

Оценить устойчивость склона высотой Н=12,0 м. Склон сложен неокомской глиной с параметрами: , ,

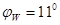С_w=12,5 кПа. Крутизна склона характеризуется углом наклона линии склона к горизонту .

Оценить устойчивость склона высотой Н=14,0 м. Склон сложен

суглинком с параметрами: , , 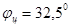С_w=90 кПа. Крутизна склона характеризуется углом наклона линии склона к горизонту .

Задача 2. Определение устойчивости откоса методом круглоцилиндрических поверхностей скольжения.

Определить коэффициент устойчивости откоса, сложенного однородным грунтом с характеристиками γ, φ, С при заданном положении кривой скольжения в виде дуги окружности с центром в точке О1.

Крутизна откоса 1:m, где m=B/H; откос нагружен равномерно распределенной нагрузкой q.

Высота откоса Н, м

γ, кН/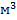

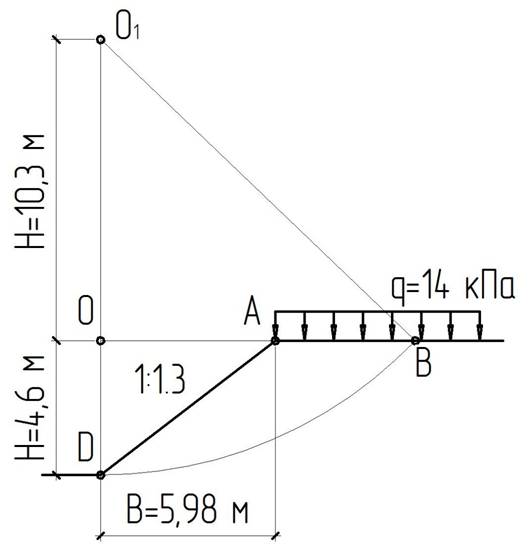
Примем координатную систему XZ; радиусом R=h+H проводим дугу окружности, выделив массив грунта DAB (рис. 2). Координаты точек: О1(0;-10.3), D(0;4.6), А(5.98;0).

Из треугольника ОО1В имеем 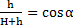, откуда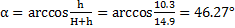

Тогда ОВ=R∙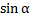=14.9∙0.72=10.77 м, а т. В имеет координаты (10.77;0).

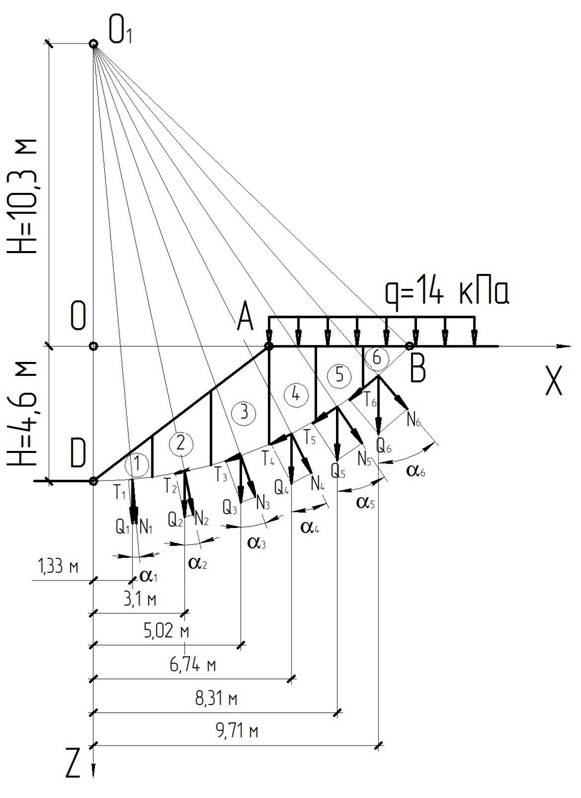
Решение проводим по алгоритму:

1. Делим массив DAB на 6 отсеков, нумеруя их снизу вверх:

b 1=b2=2 м, b3=1.8 м, b4=b5=1.6 м, b6=1.59 м

2. Записываем уравнение окружности с центром в т. О1(0;-10.3)

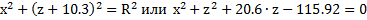
3. Вычисляем правые высоты отсеков.

Для отсека №1, используя уравнение окружности, при х1=2 м получаем z1=4.47 м

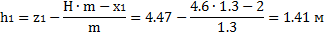
Для отсека №2, при х2=4 м получаем z2=4.05 м

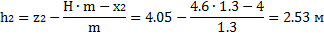
Для отсека №3, при х3=5.98 м получаем z3=3.35 м

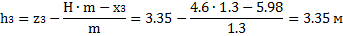
Для отсека №4, при х4=7.58 м получаем z4=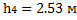

Для отсека №5, при х5=9.18 м получаем z5=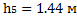

Для отсека №6, при х6=10.77 м получаем z6=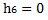

4. Определяем площади отсеков, пренебрегая кривизной поверхности скольжения в

силу незначительной разницы в длине между хордой и дугой в пределах одного отсека.

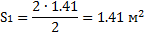
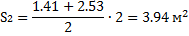
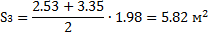
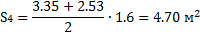
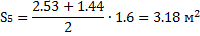
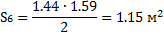
5. Определяем вес отсеков (l=1 м); для №4, №5 и №6 учитываем действие нагрузки

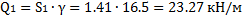
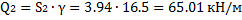
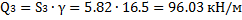
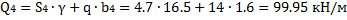
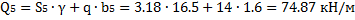
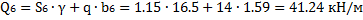
Равнодействующие Qi считаем приложенными в точках пересечения соответствующего участка дуги скольжения и вертикальной линии, проходящей через центр тяжести отсека, т.е. в точках с абсциссами:

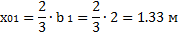
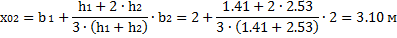
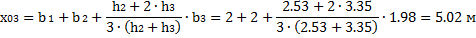
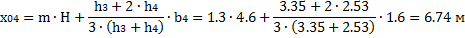
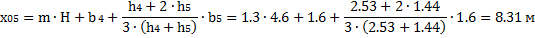
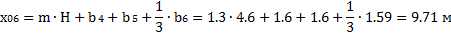
6. Определяем центральные углы αi между вертикалью и радиусом в точке приложения

веса отсека по формуле:

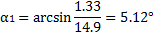
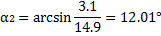
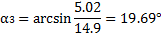
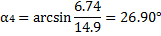
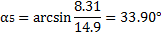
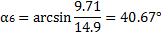
7. Центральный угол, соответствующий дуге DB:

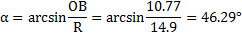
Длина дуги кривой скольжения определяется и соотношения:

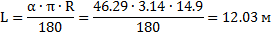
Силы Qi раскладываем на две составляющие: нормальную Ni к заданной поверхности и касательную Ti, учитывая также сцепление грунта по всей поверхности скольжения. Составляем таблицу для расчета коэффициента устойчивости.

Таблица 1. Определение составляющих сил от веса отсеков.

Укажите правильное определение коэффициента устойчивости откоса

Укажите условие устойчивости свободного откоса для идеально связанного грунта.

Укажите условие устойчивости свободного откоса для идеально сыпучего грунта

α=φ угол заложения откоса не должен превышать угла внутреннего трения

, h-мах высота устойчивого откоса с вертикальной стенкой.

3. Какой метод определения устойчивости откосов является наиболее универсальным?

4. Какое допущение из перечисленных ниже не относится к методу круглоцилиндрических поверхностей при определении устойчивости откосов?

Поверхность скольжения при обрушении круглоцилиндрической поверхности, отдельные блоки не оказывают давления друг на друга

6.Какое уравнение для определения коэффициента устойчивости откоса является правильным?

Лекция 11 Определение давления грунта на подпорные сооружения.

1. Какой тип подпорной стенки назван не правильно?

Подпорные стены по конструктивному решению подразделяются на массивные, тонкостенные и парусноготипа.

Массивные подпорные стены имеют примерно одинаковые размеры по высоте и ширине.

Устойчивость тонкостенных подпорных стен обеспечивается собственным весом стены и фунта, вовлекаемого конструкцией стены в работу, либо защемлением стен в основание (гибкие подпорные стены и шпунтовые ограждения). Тонкостенные подпорные стены: а — консольные; б — с анкерными тягами; в — контрфорсные

Схема подпорных стен парусного типа: а — с опорами из пневматических свай; б — с опорами из свай-оболочек; 1 — парус — гибкое полотнище; 2 — свая (свая-оболочка); 3 — анкерная плита

Подпорные сооружения: 1) с 2 вертикалями; 2) с вертикальной лицевой и наклонной тыльной; 3) с наклонной лицевой и вертикальной тыльной; 4) с наклоном обеих сторон в сторону засыпки; 5) с вертикальной лицевой и ступенчатой тыльной (сборное подпорное сооружение); 6)тонкостенные подпорные стенки углового типа; 7) заанкеренные подпорные и шпунтовые стенки.

2. Какое давление грунта на подпорное сооружение называется активным?

Активное давление возникает при значительных перемещениях конструкции в направлении давления и с образованием плоскостей скольжения в грунте, соответствующих его предельному равновесию

Давление со стороны грунта, находящегося в предельном состоянии по направлению смещения сооружения .

3. Какое давление грунта на подпорное сооружение называется пассивным?

пассивное давление (Е_р), появляющееся при значительных перемещениях конструкции в направлении, противоположном направлению давления и сопровождающееся началом «выпора грунта».

Пассивное давлениевозникает при перемещении подпорной стенки в сторону грунта засыпки

4. Какое допущение при определении давления грунта на подпорное сооружение практическими методами сформулировано не верно?

Активное и пассивное давление опред. исходя из предположения, что грунт находится в пред. напряженно-деформируемом сост. (т.е. в случае отсутствия подпорной стенки произойдёт обрушение откосов). Поэтому точные решения могут быть получ. по теории ПНС.

1. Поверхность скольжения призмы обрушения принимается плоской

2. Задняя стенка подпорного сооружения вертикальная

3. Засыпка грунта горизонтальная

4. Трением грунта о подпорную стенку пренебрегаем

5. Какое из уравнений для определения пассивного давления идеально сыпучего грунта на подпорное сооружение является верным?, где к-т пассивного давления

6. Какое из уравнений для определения активного давления идеально сыпучего грунта на подпорное сооружение является верным? , где к-т активного давления:

Лекция 12 Деформации грунтов и расчет осадок фундаментов

|	следующая лекция ==>
Укажите основные условия принципа линейной деформируемости грунта	|	Выберите правильное выражение для определения осадки однородного линейно-деформируемого полупространства

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет