Угол откоса призма обрушения

Занятие 3. МЕТОДИКА РАСЧЕТА ДАВЛЕНИЯ СЫПУЧЕГО ТЕЛА НА ОГРАЖДЕНИЯ

Скачать:

«Задача о распределении напряжений внутри сыпучего тела и на его поверхности соприкосновения с другими телами принадлежит к числу труднейших задач строительной механики» /Рабинович И.М./ [9] .

Сложность и неопределённость задачи состоят в том, что частицы, образующие упругое тело, имеют различную величину и форму, различную твердость и шероховатость; что между ними действуют силы трения, которые, в свою очередь, меняются в зависимости от степени влажности сыпучего тела. Кроме сил трения, действуют еще более неопределенные силы прилипания (сцепления).

Значительные изменения величины и направления давления земли вызывают: способ и последовательность засыпки земли позади ограждения, естественное и искусственное трамбование, случайные или систематические сотрясения грунта, малейшие осадки и перемещения стенки под влиянием собственного веса.

Становится ясно, насколько трудно в данном случае разработать приемлемые теории расчета. Поэтому все теории, предложенные до настоящего времени, оперируют с идеальным сыпучим телом (моделью), наделенным некоторыми гипотетическими однородными свойствами.

Существующие в настоящее время основные методы расчета давления сыпучего тела на ограждения основаны на предложенной в восемнадцатом веке теории Ш.О. Кулона (рис. 1, а), вошедшей в историю под кратким названием «теория Кулона». Далее рассмотрим, в чём она состоит.

1. ТЕОРИЯ КУЛОНА

Вначале перечислим упрощающие гипотезы, на которых эта теория основана:

1. Сыпучее тело (земляная масса) рассматривается как однородная сплошная среда, способная воспринимать только сжимающие и сдвигающие усилия;

Рис. 1. Учёные – инженеры, разработавшие практические методы расчёта давления сыпучего тела на ограждения

а — Кулон Шарль Огюстен (1736 — 1806): французский военный инженер. В 1781 г. сформулировал законы сухого трения;
б — Ребхан Георг (1824 — 1892): Венский профессор, инженер – строитель;
в — Понселе Жан Виктор (1788-1867): французский математик и инженер. Заложил основы проективной геометрии

2. Принимается, что при равновесии результирующее напряжение на любой площадке внутри сыпучего тела может отклоняться от нормали к площадке на угол, не превышающий некоторой величины α, которая зависит от физических свойств данного сыпучего тела. (Мы уже знаем, что этот угол равен углу внутреннего трения φ);

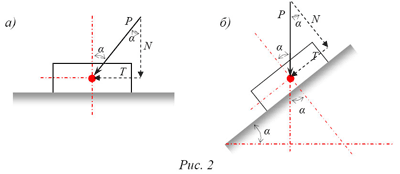
Схема к оценке состояния равновесия тела на плоскости а – горизонтальная плоскость; б – наклонная плоскость;

* Если на тело, способное скользить по плоскости, действует сила Р, наклоненная к нормали по углом α, то нормальная составляющая имеет величину N=P·cos α, сила трения из условия равновесия не может превысить величины N·f 1 = P·f ·cos α (рис. 2). Кроме того, сдвигающая сила равна T=P·;sin α. До тех пор, пока T 1 Здесь f – коэффициент трения, f = tgφ.

3. Предполагается, что стенка, уступая давлению сыпучего тела, начинает отодвигаться и определяется не то давление, которое она испытывает при обычных условиях, а то предельное, которое отвечает первому мгновению процесса отодвигания стенки. Кулон считал, что давление на стенку при обычных условиях не может превысить того, которое отвечает моменту нарушения равновесия и началу обрушения;

4. Принимается следующая гипотеза разрушения системы стенка- грунт: от сыпучего тела отделяется клин, ограниченный с одной стороны поверхностью подпорной стенки, а с другой стороны – плоскостью, проходящей через основание стенки (см. рис. 1). Эта плоскость называется плоскостью обрушения или плоскостью скольжения, а клин – призмой обрушения. Сам клин рассматривается при этом как абсолютно твёрдое тело;

5. Задача решается в условиях «плоской задачи»: предполагается, что стенка имеет неограниченную длину, и что профиль земляной массы и все прочие условия остаются по длине стенки постоянными. Таким образом, расчет ведется для участка стенки длиной 1м. Призма обрушения имеет при этом высоту, также равную единице (1м).

Наметив ограничения, мы вплотную подошли к сути теории.

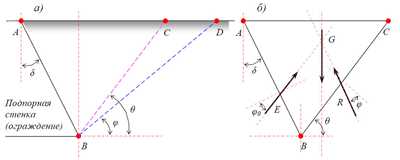
Рис. 3. Схема к определению давления сыпучего тела на ограждение а – формирование призмы (клина) обрушения; б – призма обрушения, отделённая от внешней среды

1. рассмотрим давление, оказываемое на некоторый участок АВ подпорной стенки (рис. 3);

2. проведем плоскость естественного откоса ВD;

3. вообразим, что линия ВС есть след плоскости обрушения, угол ее наклона к горизонту обозначим через θ;

4. призма обрушения «сползает» по поверхности ограждения и некоторой плоскости обрушения ВС;

5. рассмотрим момент начала сползания, когда связи между грунтом и ограждением ещё существуют, но напряжение в них – максимально. К этому случаю применяются условия равновесия, поэтому выделим призму обрушения и заменим действие отброшенных связей равнодействующими: E – в связях между ограждением и сыпучим телом; R – в связях между частицами сыпучего тела по поверхности обрушения (рис. 3, б);

6. Кроме реакций в связях, на призму обрушения действует её собственный вес (пригрузка на поверхности здесь не рассматривается): G = пл. тр. ABC · γ (здесь γ – удельный вес грунта, кН/м 3 );

7. В момент нарушения равновесия, когда клин начнет сползать вниз, преодолевая силы трения (силы сцепления приняты равными нулю) равнодействующие отклонятся от перпендикуляра к поверхности на соответствующий угол трения (рис. 3,б, рис. 4,а): φ – для поверхности обрушения ВС («грунт по грунту») и φ – для поверхности стенки – «грунт по стенке» (угол трения грунта о стенку часто принимают равным нулю: т.е. стенка принимается идеально гладкой);

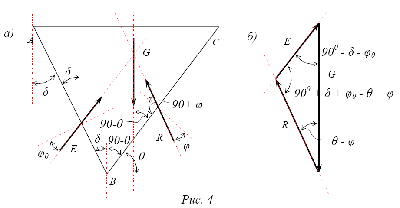
Равновесие призмы обрушения а – силы, действующие на призму обрушения; б – треугольник сил

8. Три силы – E, R и G находятся в равновесии, если они пересекаются в одной точке и треугольник сил – замкнут (рис. 4,б). Нас интересует сила E, которая противоположна давлению земли на ограждение;

9. Далее по теореме синусов:

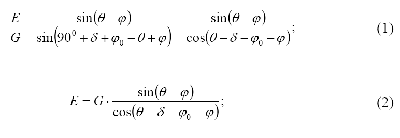
10. Однако в правую часть выражения (2) входит неизвестный угол θ, который определяет также и вес призмы обрушения G. То есть θ является единственной независимой переменной в этой формуле. Каждому значению этого угла соответствует новое положение плоскости обрушения, новое значение веса призмы G и новое значение силы E. Необходимо определить то значение θ, при котором величина E достигает максимума. Такое значение существует, т.к. при совпадении линий ВС и ВD (когда θ = φ) призма обрушения лежит на естественном откосе и, являясь абсолютно твердым телом (см. гипотезы), не давит на стенку. В то же время при совпадении линии ВС с АВ призма обрушения не существует, следовательно G = 0 и E = 0. То есть искомая точка C лежит где-то между точками А и D.

Далее рассмотрим несколько удачных примеров дальнейшего развития теории Кулона.

ПРИЛОЖЕНИЕ 3
Рекомендуемое

1. Для определения крутизны откоса принимаем буквенные обозначения величин:

h — высота откоса, м ;

q — крутизна (угол) откоса, град;

с и j — предельные значения удельного сцепления, кПа, и угла внутреннего трения, град, определяемые по формулам:

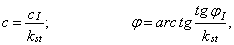(1)

где c _I и j _I — расчетные значения соответственно удельного сцепления, кПа, и угла внутреннего трения, град, определенные согласно требованиям СНиП 2.02.01-83;

k_st — коэффициент устойчивость, определяемый по формуле

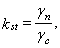(2)

здесь g _n и g _c — соответственно коэффициенты надежности по назначению и условий работы, принимаемые в соответствии со СНиП 2.02.01-83; для земляных сооружений высотой (глубиной) до 10 м со сроком службы до 5 лет допускается принимать значение коэффициента надежности по назначению g _n = 1,05;

g _I — расчетное значение удельного веса грунта, кН/м 3 , определяемого в соответствии с требованиями СНиП 2.02.01-83. Удельный вес, кН/м 3 , вычисляется путем умножения плотности, т/м 3 , на величину ускорения силы тяжести, 9,8 м/с 2 .

2. Находим число единиц загружения K в заданной нагрузке q , кПа, на поверхности грунтового массива по формуле

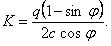(3)

При отсутствии нагрузки на поверхности или ее расположении от бровки выемки на расстояниях, больше установленных в п. 5 , принимается К = 0.

3. Определяем параметр устойчивости по формуле

4. Требуемый угол откоса q находим по значениям j , К и Е следующим образом:

при Е £ 0,25 по графикам на черт . 1-5 с интерполяцией для промежуточных значений j и Е;

при Е > 0,25 по формуле

где q — предельное значение q (обозначено на верхнем обрезе координатной сетки на черт. 1-5 );

q _0,25 — значение q , соответствующее Е = 0,25.

5. Для временных откосов (со сроком службы до одного года) минимальное приближение к бровке b_f , м, нагрузки, которую допускается не учитывать ( К = 0) при нахождении значения q , допускается определять в зависимости от ширины призмы обрушения откоса b , м:

а) при нагрузке от сыпучего материала с удельным весом g _m £ 18 кН/м 3 (например, от отвала грунта), отсыпанного под углом естественного откоса, но не более 45 от горизонтали

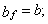(6)

б) при равномерно распределенной нагрузке

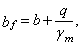где g _m = 18 кН/м 3 . (7)

Ширину призмы обрушения откоса b , м, определяем по формулам:

при Е ³ 0,167 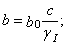(8)

при 0,167 > Е ³ 0,1

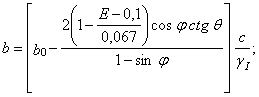(9)

при Е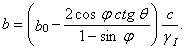

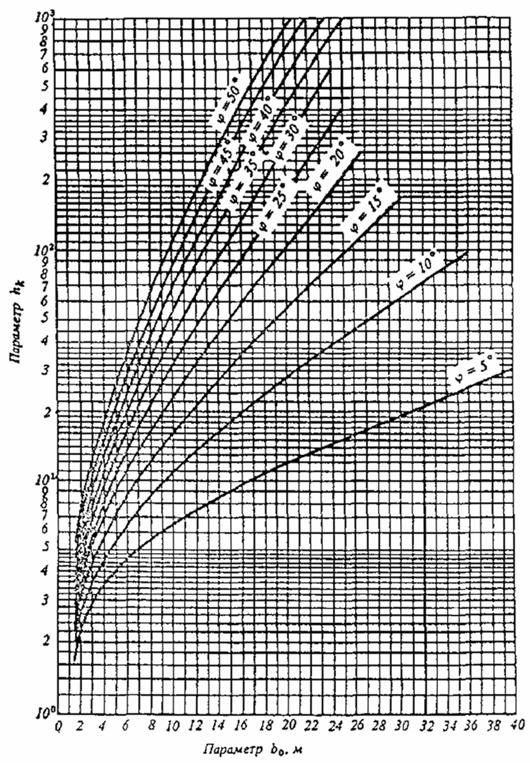
Параметр b находим по черт. 6 в зависимости от параметра h_k , определяемого по формуле

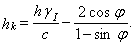(11)

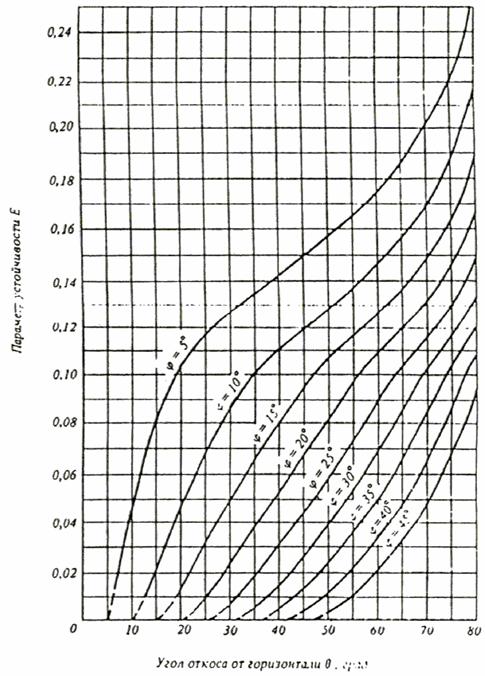
Черт. 1. Графики для определения крутизны откоса при К = 0

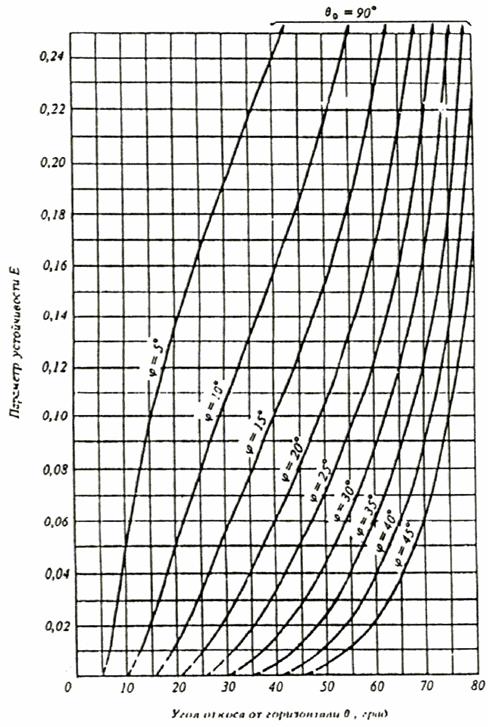
Черт. 2. Графики для определения крутизны откоса при К = 1

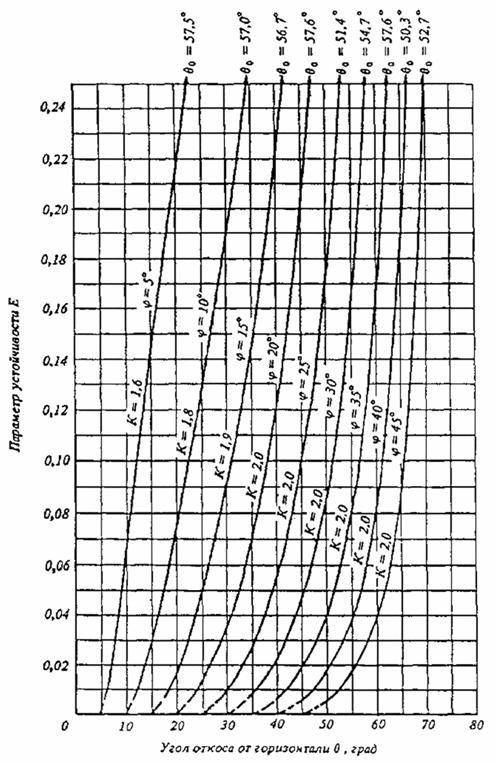
Черт. 3. Графики для определения крутизны откоса при 1

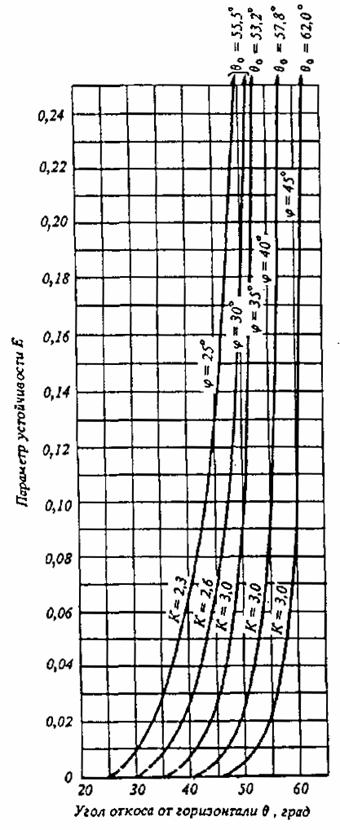
Черт. 4. Графики для определения крутизны откоса при 2

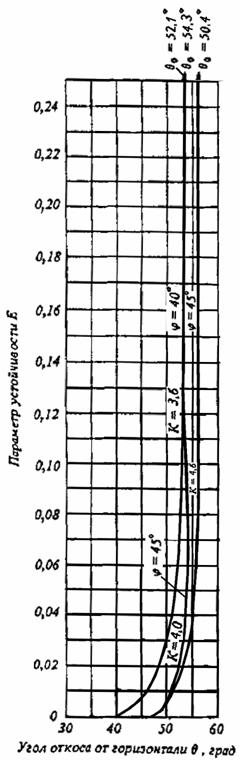
Черт. 5. Графики для определения крутизны откоса при 3 K

скважин на воду, лицензия на недропользование, как оформить лицензию, подача документов в департамент роснедра»>http :// soyuzproekt . ru Бурение скважин под свайный фундамент . Бурение водопонижающих скважин (либо осущающих скважин ) и обустройство их необходимым насосным оборудованием с автоматикой. Бурение под буроинъекционные сваи, бурение под буронабивные сваи. Скважины различных диаметров.

Устройство откосов земляных сооружений

Основными элементами открытой разработки карьера, котлована или траншеи без крепления являются: сторона — l; высота уступа — H; форма уступа; угол откоса — а; крутизна (рис. 7.1).Обрушение откоса происходит чаще всего по линии АС, расположенной под углом Θ к горизонту. Объем АВС называют призмой обрушения.Призма обрушения удерживается в равновесии силами трения, приложенными в плоскости сдвига. Перед разработкой траншей и котлованов необходимо заранее определить крутизну откосов, обеспечив безопасность вроведения работ, с учетом глубины траншеи или котлована и выбрать способ формирования откосов. Рытье котлованов и траншей с откосами без креплений в нескальных грунтах выше уровня грунтовых вод (с учетом капиллярного поднятия) или в грунтах, осушенных с помощью искусственного водопонижени допускается с соблюдением нормативной глубины выемки и крутизны откосов .

Перед открытием котлованов и траншей без откосов, не зависимо от вида грунта, расчетным путем необходимо определить их максимально безопасную глубину, что обеспечивает устойчивость вертикальных стенок. Методика расчета безопасной глубины котлованов и траншей без откосов такова:

1. Рассчитывают критическую высоту вертикальной стенки котлована (траншеи) по формуле:

где Н — критическая высота вертикальной стенки, м; С — сила сцепления почвы, т/м2; γ — объемный вес грунта т/м3; φ — угол в нутреннего трения

2. Определяют предельную глубину котлована или траншеи с вертикальной стенкой, вводят коэффициент запаса, принимаемый равный 1,25:

где Н_пр — предельная высота вертикальной стенки, м.

Глубина разработки котлованов и траншей с вертикальными стенками без креплений устанавливается в соответствии с ДБН А.3.2.2-2009 и составляет не более 1 м в насыпных, песчаных, крупнообломочных грунтах; 1,25 м, в супесях, 1,5 м в глинах. При проектировании котлованов и траншей глубиной более 5м необходимо произвести расчет устойчивости откосов. Согласно ДБН А.3.2.2-2009, перемещение, установка и работа машин вблизи выемок с незакрепленными откосами разрешается только за пределами призмы обрушения на расстоянии, установленной проектом производства работ. При отсутствии решений в ППР наименьшее расстояние до ближайших опор машин выбирается по табл. 4.4. При глубине выемки менее 5 м наименьшее допустимое расстояние от верхнего строения пути (конца шпалы, гусеницы, колеса) до основанию откоса определяется по приближенной оценке заднего края призмы обрушения с использованием формулы:

l _н = 1,2ah + 1,

где h — глубина выемки, м, а — коэффициент заложения откоса, который принимается по данным табл. 5.2.

Характеристики ґрунта

studopedia.org — Студопедия.Орг — 2014-2021 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.001 с) .

Призма обрушения

При́зма обруше́ния (англ. sliding triangle , англ. sliding wedge ) — неустойчивая часть массива уступа со стороны его откоса, заключённая между рабочим и устойчивым углами откоса уступа [1] .

Понятие призмы обрушения используется при расчётах откосов [2] , устойчивых к обрушению и предотвращения оползней.

Содержание

См. также

• Земляные работы
• Оползень
• Сваи
• Угол естественного откоса

Примечания

1. ↑Призма обрушения
2. ↑Источник: А. З. Абуханов, «Механика грунтов»: Устойчивость откосов

Литература

• А. З. Абуханов, «Механика грунтов»
• Шубин М. А. Подготовительные работы при сооружении земляного полотна железной дороги. — М .: Транспорт, 1974.

Ссылки

• СНиП 2.06.05-84 Плотины из грунтовых материалов: РАСЧЕТ УСТОЙЧИВОСТИ ОТКОСОВ ПО СПОСОБУ НАКЛОННЫХ СИЛ ВЗАИМОДЕЙСТВИЯ
• СНиП 2.09.03-85 СООРУЖЕНИЯ ПРОМЫШЛЕННЫХ ПРЕДПРИЯТИЙ
• Источник: А. З. Абуханов, «Механика грунтов»: Устойчивость откосов
• Методы расчета устойчивости откосов
• Давление земли // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб. , 1890—1907.
• Рисунок: Схема откоса грунта: 1 — откос; 2 — линия скольжения; 3 — линия, соответствующая углу внутреннего трения; 4— возможное очертание откоса при обрушении; 5 — призма обрушения массива грунта

Wikimedia Foundation . 2010 .

• Призма Синаххериба
• Признавшимся

Полезное

Смотреть что такое «Призма обрушения» в других словарях:

Призма обрушения борта карьера (откоса уступа, отвала) — 45. Призма обрушения борта карьера (откоса уступа, отвала) часть массива горных пород (отвальных масс), заключенная между бортом карьера (откосом уступа или отвала) и поверхностью скольжения. Достигнув состояния предельного равновесия, призма… … Официальная терминология

Давление земли — Сухая свеженасыпанная земля, лишенная сцепления, удерживается в равновесии, как и вообще всякое сыпучее тело, под действием силы тяжести и трения; самый крутой откос, который можно придать земле в этом случае, называется естественным, или… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

Угол естественного откоса — Угол естественного откоса угол, образованный свободной поверхностью рыхлой горной массы или иного сыпучего материала с горизонтальной плоскостью. Иногда может быть использован термин «угол внутреннего трения». Частицы мате … Википедия

Чернобыльская авария — Координаты: 51°23′22.39″ с. ш. 30°05′56.93″ в. д. / 51.389553° с. ш. 30.099147° в. д. … Википедия

ГОСТ Р 54523-2011: Портовые гидротехнические сооружения. Правила обследования и мониторинга технического состояния — Терминология ГОСТ Р 54523 2011: Портовые гидротехнические сооружения. Правила обследования и мониторинга технического состояния оригинал документа: 3.7.1 акватория порта: Водная поверхность порта в установленных границах, включающая в себя… … Словарь-справочник терминов нормативно-технической документации

РБМК — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия