Что такое криволинейный откос

Что такое криволинейный откос

Рассмотрим решения в проекциях с числовыми отметками некоторых примеров, встречающихся при выполнении задачи 11 контрольной работы №2.

На рис.7 показано построение линии пересечения плоскостей и . Такая задача может встретиться при определении линии пересечения плоских откосов насыпей или выемок. Искомая проекция линии пересечения плоскостей и проходит через точки пересечения двух пар «одноименных» (с одинаковыми отметками) горизонталей заданных плоскостей.

Линия пересечения плоскости с поверхностью конуса будет проходить через точки пересечения одноименных горизонталей этих поверхностей. Решение этой задачи также встречается в практике строительного проектирования и в контрольной работе №2, так как откосы насыпей или выемок могут иметь коническую форму. На рис.8 показан пример решения такой задачи. Проекция линии пересечения конической поверхности с плоскостью проходит через точки .

Линия пересечения топографической поверхности с горизонтально — проецирующей плоскостью (рис.9) носит название профиля топографической поверхности. Построение этой линии — распространенная в строительном проектировании задача. Для ее решения рекомендуется следующий практический прием. К проекции плоскости , ее горизонтальному следу прикладывается полоска бумаги, куда переносятся точки пересечения плоскости с горизонталями топографической поверхности . Полученные точки переносят на горизонтальную линию — основание профиля, отметку которой задают условно. В данном случае отметка основания 3,00. Затем в масштабе чертежа из отмеченных точек откладывают по перпендикуляру вверх превышения отмеченных точек (разность отметки точки и принятой отметки основания профиля). Искомая линия профиля (сечения плоскости с топографической поверхностью) будет проходить через точки .

На рис.10 заданы топографическая поверхность и горизонтальный участок полотна дороги, отметка которого 12,00 м. Дорога будет расположена на насыпи, так как отметки горизонталей местности (топографической поверхности) меньше отметки полотна дороги. Требуется определить границы насыпи дороги. Уклон откосов насыпи задан и равен 1:1,5, поэтому интервал плоскостей откосов насыпи будет равен 1,5 м. Граница насыпи пройдет через точки пересечения одноименных горизонталей откосов насыпи и топографической поверхности. Проводим параллельно бровке дороги горизонтали плоскости южного откоса насыпи и отмечаем точки , через которые проходит искомая линия. Аналогично строится линия пересечения топографической поверхности с северным откосов насыпи.

На плане берг-штрихами показывают направление ската воды вдоль откосов. Берг-штрихи изображаются сплошной тонкой линией через 2. 5 мм (рис.10).

На рис.11 та же задача решена для горизонтального участка дороги, расположенного на круговой кривой. Откосы насыпи в этом случае имеют коническую форму, а горизонтали откосов — концентрические окружности. Граница откоса насыпи будет проходить через точки , где пересекаются горизонтали конического откоса с одноименными горизонталями топографической поверхности.

Несколько сложнее решается эта задача для случая, когда дорога расположена на наклонном участке (см. рис.12). В этом случае горизонтали плоского откоса не будут параллельны бровке дороги, так как она будет наклонная. Горизонтали откосов насыпи будут касательны к одноименным горизонталям конусов с вершинами, принадлежащими бровке полотна дороги, образующие которых имеют тот же уклон, что и откосы насыпи. Например, на рис.12 вершины конусов расположены в точках . Горизонталь южного откоса насыпи с отметкой 11 проходит через точку с отметкой 11, расположенную на бровке полотна и касательную к горизонтали конуса с отметкой 11. Остальные горизонтали откоса насыпи будут параллельны проведенной горизонтали с отметкой 11. Искомая линия пересечения пройдет через точки пересечения одноименных горизонталей насыпи и топографической поверхности . Также строится и граница северного откоса насыпи. Аналогично решается эта задача и для случая, когда дорога расположена в выемке, разница только в том, что отметки горизонталей по мере удаления от бровки полотна будут не уменьшаться, а возрастать.

ПРИМЕРЫ РЕШЕНИЯ КОНТРОЛЬНЫХ ЗАДАНИЙ 1

Пример решения задачи 11 для студентов специальности ПГС приведен на рис.13, на котором задана топографическая поверхность и расположенная на ней горизонтальная строительная площадка с отметкой 28, а также наклонный въезд на площадку (аппарель). Заданы уклоны насыпи 1:1,5; выемки 1:2 и дороги (аппарели) 1:5.

Часть площадки, расположенная к западу от 28 горизонтали топографической поверхности, будет расположена в выемке, а к востоку от этой горизонтали — на насыпи. Проекции горизонталей плоских откосов площадки будут прямые, параллельные ее бровке и отстоящие друг от друга на 1,5 м в масштабе чертежа для насыпи и на 2 м для выемки. Построение линий пересечения их с топографической поверхностью сводится к решению примера, рассмотренного на рис.10.

Поверхность выемки, примыкающей к криволинейной части площадки, будет конической, а горизонтали откоса этой части выемки будут концентрическими окружностями, расстояния между которыми (интервалы) будут 2 м. Построение линии пересечения конического откоса с топографической поверхностью показано на рис.11.

Аппарель (наклонный въезд на площадку) имеет уклон, горизонтали аппарели будут расположены на расстоянии 5 м друг от друга, а горизонтали откосов насыпи аппарели будут касательны к горизонталям конусов, имеющих вершины на бровке аппарели. Граница откосов насыпи аппарели строится аналогично построениям, приведенным на рис. 12.

Линия пересечения откосов конической и плоской частей выемки пройдет через точки и будет криволинейной (часть параболы). Линия пересечения плоскостей откосов, имеющих одинаковый уклон будет проецироваться по биссектрисе угла между горизонталями плоскости (см., например, линию ). Восточный откос площадки и южный откос аппарели пересекаются по прямой . Аналогично строятся и другие участки искомых линий.

При построении линий пересечения откосов с топографической поверхностью часто приходится определять точки, принадлежащие этой линии и расположенные вне пределов рассматриваемых откосов, например, точки на рис. 13 или точки на рис. 14. Эти точки вспомогательные, необходимые для построения границы земляных работ на участках непосредственно прилагающих к линиям пересечения откосов.

Профиль местности строят аналогично примеру, рассмотренному на рис.9. На профиле показывают попавшие в секущую плоскость контуры горизонтальной площадки, наклонной дороги и откосов насыпи и выемки.

Пример решения задачи 11 для студентов специальностей С, МТ и ВК показан на рис.14. Здесь задана топографическая поверхность и полотно дороги с горизонтальным криволинейным участком радиуса и отметкой 28 и наклонным, прямолинейным участком имеющим уклон 1:5.

Определив интервалы наклонного участка дороги — , выемки и насыпи — , проводят горизонтали аппарели и откосов. Часть дороги, расположенная восточнее горизонтали местности с отметкой 28, будет находиться на насыпи, а западнее этой горизонтали — в выемке. Затем строят линию пересечения откосов горизонтального и наклонного участков, дороги (см. линии и на рис.14). Построение линии пересечения откосов насыпей и выемок дороги с топографической поверхностью на прямолинейном участке дороги аналогично рис.12, а на криволинейном — рис. 11.

ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ ЗАДАНИЯ № 1

1. Подготовить формат А-3 (изобразить рамку, основную надпись, размеры которой приведены на рис. 13).

2. Над основной надписью изобразить линейный масштаб Ml:200 (1 м на местности должен соответствовать 5 мм чертежа).

3. Разметить положение горизонталей рельефа местности в соответствии с вариантом и провести их сплошными тонкими линиями. Для этого чертеж задание необходимо увеличить в 4 раза (если методика на формате А4).

4. Студентам специальности ПГС нанести на плане контуры строительной площадки и аппарели, положение которых должно соответствовать исходным данным таблицы 2 подвариантов.

Студентам специальностей С, МТ, ВК изобразить на плане местности контуры горизонтального криволинейного участка дороги радиуса R и наклонную аппарель. Центр дуги радиуса R должен располагаться так, чтобы ось дороги пересекала горизонтали топографической поверхности под углом близким к 90°. Поэтому центр дуги радиуса может располагаться либо вверху, либо внизу формата в зависимости от значения угла .

Точки нулевых работ целесообразно назначить в пределах горизонтального (криволинейного) участка дороги.

5. Используя линейный масштаб, над основной надписью построить график линейных уклонов насыпи — = 1:1,5; выемки — = 1:2 и аппарели = 1:5 и определить интервалы — , , .

6. Определить точки нулевых работ, как точки пересечения горизонтали местности с одноименной отметкой с контуром строительной площадки или дороги. Также определить места расположения насыпей и выемок.

7. Построить масштабы уклонов поверхностей откосов насыпей, выемок, обозначить числовые отметки.

8. Построить горизонтали аппарели, откосов и линии их пересечения.

9. Определить точки пересечения горизонталей топографической поверхности с горизонталями откосов, построить границы откосов насыпей и выемок.

10. По направлению ската воды откоса изобразить берг-штрихи.

11. Обвести линии пересечения откосов насыпей и выемок с топографической поверхностью, сплошной толстой линией.

12. В нижней части формата слева от основной надписи построить профиль строительной площадки или дороги в соответствии с вариантом положения секущей плоскости.

13. Оформить эпюр в соответствии с требованиями, приведенными в разделе «оформление контрольной работы №2».

Что такое криволинейный откос

Ветровая волна при подходе к откосу плотины на глубине, соответствующей критической, разрушается. Очертание волны в этот момент характеризуется схемой, приведенной на рисунке 22.

Рис. 22. Разрушение волны на откосе

Критическая глубина Н_кр, на которой происходит разрушение волны, определится по формуле:

(39)

Точка пересечения критической глубины с откосом принимается за начало координатных осей, относительно которых вычисляются вспомогательные величины, необходимые при построении эпюры волновых воздействий.

Возвышение точки А (рис. 22), характеризующей положение струи в начальный момент ее сброса с гребня волны, относительно начала координат находят по зависимости:

(40)

где h_гр — высота гребня волны, отсчитываемая от статического уровня, определится по эмпирической формуле:

(41)

Горизонтальная скорость струи в точке А на гребне волны равна

(42)

где Н — глубина воды перед откосом сооружения;
п — эмпирический коэффициент, вычисляемый по формуле:

(43)

Максимальная скорость струи при ударе ее об откос будет соответствовать точке В, координаты которой при данных осях определяют по формуле:

(44)

(45)

Значение максимальной скорости в точке В равно

(46)

где — коэффициент, учитывающий уменьшение скорости при растекании струи в скатывающемся потоке, равный

(47)

Разрушившаяся волна производит на покрытие гидродинамическое давление, которое может быть изображено в виде эпюры, имеющей две несимметричные ветви криволинейного очертания. При расчете покрытий откосов земляных плотин криволинейное очертание эпюры заменяют прямолинейным, учитывая, что такая замена не вносит существенных погрешностей, но значительно упрощает все расчеты.
Построение эпюры волновых давлений ведут по пяти характерным точкам — В, 1, 2, 3 и 4 (рис. 23).

Рис. 23. Эпюра волнового давления на откос в момент удара волны

Максимальное волновое давление от удара струи в момент ее обрушения находится в точке В и определится по формуле:

(48)

где — скорость струи при ударе ее об откос, вычисляемая по формуле (46);
— угол между касательной к направлению струи в точке В и нормалью к откосу, равный

(49)

— угол между касательной к направлению струи в точке В и горизонталью, определяемый из уравнения:

(50)

Давления, соответствующие точкам 1 и 3, принимают равными , а давление в точках 2 и 4 — . Положение точек 1, 2, 3 и 4, отсчитываемых по образующей откоса от точки В, находят из следующих зависимостей:

где значение S равно

(52)

Определение максимального волнового давления и построение эпюры давлений по приведенным формулам требуют выполнения трудоемких вычислительных операций, которые усугубляются еще и тем, что приходится использовать гиперболические функции. При проектировании ответственных сооружений не приходится считаться со сложностью вычислений, для неответственных же сооружений или для выполнения предварительных расчетов и получения ориентировочных значений можно воспользоваться более простыми приближенными зависимостями.

По исследованию П. А. Шанкина, эпюра волнового давления принимается прямолинейного очертания с расположением характерных точек, для которых определяют ординаты давлений, симметрично относительно точки В, которой соответствует максимальное волновое давление (рис. 24).

Рис. 24. Эпюра волнового давления по П. А. Шанкину

Положение точки В относительно статического уровня определится по формуле:

(53)

где е отсчитывают по вертикали, а точку В находят на пересечении с откосом. Практически е находится в узком интервале, определяемом из выражения:

(54)

Ордината максимального давления в точке В равна

(55)

Промежуточные ординаты давлений при построении эпюры вычисляют для четырех точек, симметрично расположенных относительно В (рис. 24) на расстоянии

(56)

Волновое давление для промежуточных точек принимается в долях от ртах по следующим зависимостям:
для точки 1

(57)

(58)

Для точек 2 и 4 ординаты давлений одинаковы и выражаются равенством:

(59)

Наряду с гидродинамическим давлением при воздействии обрушившейся волны на откос действует также статическое давление потока воды, скатывающейся от разбитой предыдущей волны. Эпюру статического давления принимают в виде треугольника (рис. 25) и строят по трем точкам.

Рис. 25. Эпюра статического давления скатывающегося с откоса потока воды.

Ординаты давлений этой эпюры вычисляют по эмпирическим формулам.

Для точки О, соответствующей началу координатных осей, ордината равна

(60)

Для точки В, отвечающей максимальному гидродинамическому давлению, ордината равна

(61)

Для точки С, определяемой пересечением статического уровня с откосом, ордината

(62)

Таким образом, при расчете плит покрытия откосов на прочность учитываются две эпюры давлений, ординаты которых в сходных точках складываются. Так, для точки В (рис. 22) суммарная ордината равна

(63)

где определится по формуле (55), а — по формуле (61).

Большая Энциклопедия Нефти и Газа

Откос — плотина

Откосы плотины назначаются в зависимости от свойств грунта, образующего тело плотины, и от ее высоты. [1]

Принятые предварительно откосы плотин проверяются статическим расчетом. [3]

Уклоны и форма откосов плотины назначаются в зависимости от ее высоты и рода грунта, из которого она выполнена, типа плотины и характеристики основания, действующих на откос сил и условий производства работ. [5]

Располагаются мачты на откосах намываемой плотины или дамбы, причем с повышением отметок уровня намываемого сооружения мачты соответственно перемещаются. Поскольку — монтаж, труб производится с помощью крана-трубоукладчика, рекомендуется последний использовать также для монтажа прожекторных мачт. [6]

Широко распространено наложение на напорные откосы плотин ( каналов) условия г э — Кх const, позволяющего построить область изменения функции Жуковского. В этом случае откос, очевидно, также оказывается криволинейным. [7]

Особое внимание следует Обращать на то, чтобы лед не разрушал крепление откосов плотины и каналов каменной отмос-ткой и не повредил затворы в водосбросах и водозаборах, а также другие элементы сооружений. [8]

Особое внимание следует обращать на то, чтобы лед не разрушал крепление откосов плотины и каналов и не повредил затворы в водосбросах и водозаборах, а также другие элементы сооружений. [9]

Среди функций (10.3) должны найтись такие, которые дадут форму откосов, близкую к форме откосов действительных плотин . [10]

В соответствии с техническими условиями задают отметку и ширину гребня, а также уклоны сухого и мокрого откосов плотины . По этим данным и по горизонталям плана намечают границы гребня и основания тела плотины, водосбросные каналы и другие элементы плотины. [11]

Со стороны верхнего бьефа ( на верхнем откосе плотины) депрессионная поверхность непрерывно сопрягается со свободной поверхностью воды в верхнем бьефе. На задний же откос плотины депрессионная поверхность, как правило, выходит выше уровняводыв нижнем бьефе, и образуется так называемый промежуток высачивания, на котором давление также равно атмосферному. [12]

ЭКРАН ПЛОТИНЫ, противофильтрационное устройство, расположенное по верх, откосу плотины . [13]

Асфальтобетон для облицовки плотин можно приготовлять на обычных установках получения горячих смесей, используемых в дорожном строительстве. Может использоваться и обычное оборудование для укладки и укатки после соответствующей реконструкции, обеспечивающей перемещение его при помощи лебедок вверх н вниз по откосам плотины . Такая асфальтовая облицовка имеет большие преимущества при использовании ее для защиты земляных плотин, сооружаемых в районах, где отсутствуют скальные породы для каменной наброски. Гидроизоляционная облицовка плотин с засыпкой скальными породами имеет важное значение, причем для этой цели предпочтительнее применять битум, чем железобетон и сталь. [14]

Гребень плотины, расположенный на высоте 32 м, возвышается на 6 1 м над нормальным уровнем воды в Гатунском озере. Та часть откоса плотины , которая подвержена прибою волн, вызываемому сильными южными ветрами, временами господствующими на озере, была вымощена. [15]

Что такое криволинейный откос

Технические науки / 10. Горное дело

К.т.н. Долгоносов В.Н.

Карагандинский государственный технический университет, Казахстан

Аналитический способ расчета устойчивости откоса

на слабом основании ограниченной мощности

Расчетная схема откоса на слабом слое ограниченной мощности представлена на рисунке 1.

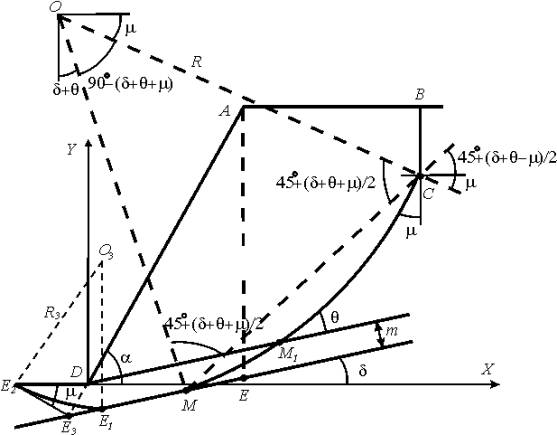
Рисунок 1 – Схема откоса на слабом основании

Для простоты решения задачи принимаем следующие допущения:

а) пренебрегаем «преломлением» поверхности скольжения в точке М₁, которое будет зависеть от разности углов внутреннего трения пород массива и слабого слоя;

б) криволинейный участок поверхности скольжения Е₁ Е₂ заменим прямой Е₃Е₂, проходящей через точку Е₃ – пересечение поверхности откоса AD с нижней границей слабого слоя ЕМ и выходящей в горизонтальную площадку у основания откоса в точке Е₂ под углом m .

Решение задачи осуществляется в следующей последовательности [1].

1) Задаем значение ширины призмы обрушения (АВ) и откладываем вниз от точки В величину Н₉₀ (точка С). С глубины Н₉₀ возникают площадки скольжения, ориентированные под углом m к линии действия главных напряжений s ₁ , которая в точке С совпадает с вертикалью.

2) По формулам, приведенным в [1] определяем значения угла входа 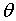. Из геометрических условий определяем координаты точек М, М₁, Е₃ и Е₂.

3) Выполняем расчеты устойчивости откоса без участия пород слабого слоя с реализацией поверхности скольжения по контакту DМ₁.

4) Выполняем расчеты устойчивости откоса с участием пород слабого слоя с реализацией поверхности скольжения по ломаному контакту МЕ₃Е₂. При этом сначала определяем устойчивость откоса по нижней границе слабого слоя (контур АВСME₃). Блок DЕ₂Е₃ выполняет функцию призмы упора (рисунок 2).

5) В случае, если контур АВСME₃ неустойчив, определяем дефицит удерживающих сил и решаем, способен ли контур DЕ₂Е₃ его компенсировать.

Рисунок 2 – Схема равновесия блока выпора слабого слоя

Максимальная несущая способность массива (по сдвигу) вдоль линии Е₂Е₃ может быть определена по формуле

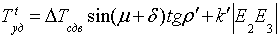, (1)

где 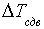— суммарная сдвигающая сила, действующая со стороны призмы АВСME₃, численно равная дефициту удерживающих сил при коэффициенте запаса .

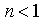Уравнения прямых, ограничивающих слабый слой

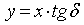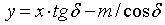; , (2)

где 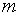— нормальная мощность слабого слоя.

Определяем координаты точек Е₂ и Е₃

;

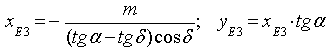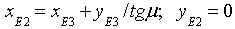. (4.3)

Интегрирование сдвигающих и нормальных сил, действующих по линиям скольжения B С M ₁ D и B С ME ₃ , осуществляется по методике, изложенной в [1] для расчетной схемы со слабым наклонным контактом.

Данная расчетная схема имеет важное практическое значение для решения задач обеспечения устойчивости карьерных откосов.

Список использованных источников

1. Долгоносов В.Н., Шпаков П.С., Низаметдинов Ф.К., Ожигин С.Г., Ожигина С.Б., Старостина О.В. Аналитические способы расчета устойчивости карьерных откосов. Караганда, Издательство «Санат-Полиграфия», 2009. 332 с.