Метод круглоцилиндрических поверхностей при расчете устойчивости откосов

Оценка устойчивости откосов методом круглоцилиндрических поверхностей скольжения. ( на эту тему мы писали последнюю расчетную задачу)

Откосы грунта могут быть как естественного сложения (берега рек, скаты горных поверхностей и т.д.), так и искусственного происхождения (насыпи, борта котлованов, траншей и т.д.).

Реальные грунты, как правило, обладают не только сцеплением, но и трением. Поэтому на практике для решения задач в строгой постановке, большое распространение получил метод круглоцилиндрических поверхностей скольжения.

Теория предельного равновесия грунтов, развитая В.В. Соколовским, позволяет решать задачи двух типов:

• задан угол наклона плоского откоса, определяется интенсивность
  внешней нагрузки на верхней горизонтальной поверхности грунта, офаниченного откосом массива;
• задана интенсивность нагрузки на верхней горизонтальной поверхности грунта, офаниченного откосом массива, определяется форма равноустойчивого откоса, находящегося в предельном напряженном состоянии.

Большое распространение на практике получил метод круглоцилиндрических поверхностей скольжения, сущность этого метода заключается в отыскании круглоцилиндрической поверхности скольжения с центром в некоторой точке О, проходящей через подошву откоса, для которой коэффициент устойчивости будет минимальным (рис. 9.9).

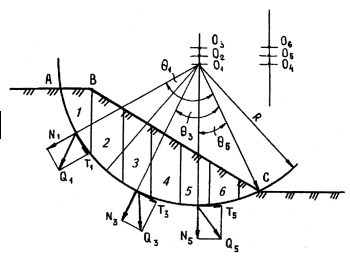
Рис. 9. 9. Схема к расчету устойчивости откоса методом круглоцилиндрической поверхности скольжения

Расчет ведется для отсека, для чего оползающий клин ABC разбивается на n вертикальных отсеков. Делается предположение, что нормальные и касательные напряжения, действующие по поверхности скольжения, в пределах каждого из отсеков оползающего клина определяются весом данного отсека Q_i, и равны соответственно:

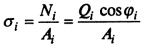(9.16)

(9.17)

Здесь
A_i — площадь поверхности скольжения в пределах i-го вертикального отсека, A_i= 1l_i; l_i — длина дуги скольжения в плоскости чертежа (см. рис. 9.9).

Препятствующее оползанию откоса сопротивление сдвигу по рассматриваемой поверхности в предельном состоянии

(9.18)

Коэффициент запаса устойчивости определим по формуле

(9.23)

Устойчивость откоса согласно изложенной расчетной методике обеспечена, если k_s>1. При проектировании сооружений коэффициент устойчивости назначают обычно в пределах 1,2—1,3.

Для решения практических задач установлен следующий порядок расчета. Из некоторого произвольного центра О₁ радиусом R через точку С проводят поверхность скольжения (см. рис. 9.9). Участок откоса, ограниченный дугой АС и ломаной линией откоса ABC, разбивают на ряд призм равной ширины, массу которых подсчитывают как площади соответствующих фигур, умноженных на удельный вес грунта. При наличии в откосе грунтов с различным удельным весом строят фиктивный профиль с удельным весом, приведенным к одному из имеющихся.

Далее по формуле (9.23) определяют коэффициент устойчивости. После того повторяют построения и расчеты при цилиндрических поверхностях скольжения, проведенных из новых центров О₂, О₃ и т.д. до тех пор, пока не будет найдено минимальное значение ks на первой вертикали. Аналогично проводят расчет, определяя минимальное значение коэффициента устойчивости для второй вертикали, строя круглоцилиндрические поверхности, проведенные из центров O₄, O₅, O₆. Затем такие же расчеты повторяют для третьей, четвертой и т.д. вертикалей, пока не будет определен самый минимальный коэффициент устойчивости. Поверхность скольжения, имеющая наименьшую величину k_s, будет наиболее вероятной поверхностью скольжения грунтов склона.

Вопрос 25-26

25Подпорные стенки. Определение активного давления грунта на подпорную стенку при различных сочетаниях «φ» и «с».

26. Подпорные стенки. Определение пассивного давления грунта на подпорную стенку при различных сочетаниях «φ» и «с».

Подпорными стенами называются сооружения, предназначенные для ограждения грунта или сыпучих тел от обрушения.

Они используются в различных областях строительства для ограждения:

• откосов, насыпей и выемок, при невозможности выполнения откосов с требуемыми уклонами;
• террас, располагаемых по генплану в различных уровнях;
• отдельных приподнятых или заглубленных по требованиям технологии участков, внутри или вне сооружений.

Также используются они для крепления котлованов, траншей, устройства водовыпусков, искусственных водоемов, водобойных колодцев и т.д.

Подпорные стены по конструктивному решению подразделяются на массивные, тонкостенные и парусного типа.

Массивные подпорные стены имеют примерно одинаковые размеры по высоте и ширине. Устойчивость массивных подпорных стен на сдвиг и опрокидывание обеспечивается их собственным весом.

Устойчивость тонкостенных подпорных стен обеспечивается собственным весом стены и фунта, вовлекаемого конструкцией стены в работу.

Массивные и тонкостенные стены можно устраивать с наклонной подошвой или с дополнительной анкерной плитой, обеспечивающей устойчивость стены при сдвиге.

В последнее время используются мягкие подпорные стенки парусного типа (рис. 10.6). Грунт засыпки поддерживается парусом, работающим на растяжение и передающим осевую сжимающую силу сваями, а растягивающую силу — анкерными плитами.

Различают следующие виды бокового давления грунта:

· активное давление (E_а) возникающее при значительных перемещениях конструкции в направлении давления и образования плоскостей скольжения в грунте, соответствующих его предельному равновесию. АБС — основание призмы обрушения, высота призмы — 1 м;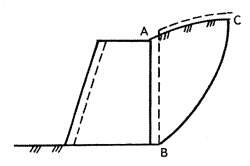

· пассивное давление (Е_р), появляющееся при значительных перемещениях конструкции в направлении, противоположном направлению давления и сопровождающееся началом «выпора грунта». АБС— основание призмы выпирания, высота призмы —1м;

Наибольшей из этих нагрузок (для одного и того же сооружения) является пассивное давление, наименьшей — активное.
Активное давление грунта вводится в качестве внешней нагрузки в расчетах на устойчивость сооружений на сдвиг и прочность гибких конструкций.
Пассивное давление учитывается как предельная реактивная сила при устойчивости и прочности сооружений, для которых горизонтальные перемещения являются допустимыми.

Активное давление грунта

Несвязный грунт

Если поверхность грунта ограничена плоскостью, то горизонтальная составляющая интенсивности активного давления несвязного грунта, определяется по формуле

(10.2)

где γ— удельный вес грунта; h — высота стенки; λ_ahφ — коэффициент активного давления,. Вертикальная составляющая интенсивности давления грунта ограниченной плоскостью определяется по формуле

(10.4)

Величина активного давления грунта (вертикальная и горизонтальная составляющая) на участок офаждающей поверхности определяется как площадь составляющей эпюры интенсивности давления. Точка приложения давления по высоте совпадает с центром тяжести соответствующего участка эпюры интенсивности давления

Связный грунт

Горизонтальная и вертикальная составляющие интенсивности активного давлениядля определения связного грунтаопределяются по формулам

Равнодействующая горизонтального и вертикального давлений связного грунта определяется по формулам

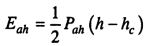
Пассивное давление грунта

Как указывалось выше, пассивное давлениевозникает при перемещении подпорной стенки в сторону грунта засыпки.

Метод круглоцилиндрических поверхностей скольжения.

Метод круглоцилиндрических поверхностен скольжения широко при­меняется на практике, так как дает некоторый запас устойчивости и ос­новывается на опытных данных о форме поверхностей скольжения при оползнях вращения, которые на основании многочисленных замеров в натуре принимают за круглоцилиндрические, при этом самое невыгодное их положение определяется расчетом. Принятие определенной формы поверхностей скольжения и ряда других допущений (о чем будет сказано ниже) делает этот метод приближенным.

Рис. 4.18. К расчету устойчивости откоса по круглоцилиндрическим по­верхностям скольжения: а —схема действия сил;

Допустим, что центр круглоцилиндрической поверхности скольжения оползающей призмы находится в точке О (рис. 4.18, а). Уравнением равновесия будет ΣМ = 0. Для составления уравнения моментов относительно точки вращения О разбивают призму скольжения ABC вертикальными сечениями на ряд отсеков и принимают вес каждого отсека условно приложенным в точке пересечения веса отсека Р_i с соответствующим отрезком дуги сколь­жения, а силами взаимодействия по вертикальным плоскостям отсека (считая, что давления от соседних отсеков равны по величине, а по направлению противоположны) пренебрегают. Раскладывая далее силы веса P_i на направление радиуса вращения и ему перпендикулярное, составляют уравнение равновесия, приравнивая нулю момент всех сил относительно точки вращения:

Сокращая это выражение на R, получим

Здесь L — длина дуги скольжения АС; φ, с — угол внутреннего трения и сцепление грунта; T_i и N_i — составляющие давления от веса отсеков, определяемые графически или вычисляемые по замерам углов α_i:

За коэффициент устойчивости откоса принимают отношение момента сил удерживающих к моменту сил сдвигающих, т. е.

(4.14)

Однако решение поставленной задачи определением коэффициента устойчивости для произвольно выбранной дуги поверхности скольжения не заканчивается, так как необходимо из всех возможных дуг поверхностей скольжения выбрать наиболее опасную. Последнее выполняется путем попыток, задаваясь различными положениями точек вращения О.

Рис. 4.18. К расчету устойчивости откоса по круглоцилиндрическим поверхностям скольжения: б – положение опасных дуг скольжения;

Для ряда намеченных центров дуг поверхностей скольжения (O_l О₂; О₃ — рис. 4.18, б) определяют необходимое по условию устойчивости сцепление, соответствующее предельному равновесию заданного откоса, по выражению, вытекающему из соотношения (у₂), а именно:

(4.15)

Далее, из всех возможных центров скольжения выбирают тот, для которого требуется максимальная величина сил сцепления. Этот центр принимают за наиболее опасный и для него по формуле (4.14) вычисляют коэффициент устойчивости η.

Обычно считают, что при значении η≥ 1,1 – 1,5 откос будет устойчивым.

Формула (4.14) будет справедлива лишь для тех случаев, когда дуга по­верхности скольжения во всех своих частях является ниспадающей в сторону возможного смещения откоса или когда все отсеки кривой скольжения располагаются по одну сторону от направления вертикального радиуса О А (рис. 4.18, в).

Рис. 4.18. К расчету устойчивости откоса по круглоцилиндрическим по­верхностям скольжения: в – схема сил, действующих по поверхности скольжения

Если обозначить сдвигающие силы, направленные в сторону скольжения (сдвига), Т _{i сдв} , а сдвигающие силы, направленные в сторону, противоположную направлению смещения (например, Т₄ и Т₅ по рис. 4.18, в), и удерживающие откос от скольжения, Т_iуд то формула (4.14) примет такой вид:

По выражению (4.14′) и следует определять коэффициент устойчивости откосов и склонов при расчетах по методу круглоцилиндрических поверхностей скольжения.

Однако, как показывают соответствующие расчеты, метод круг-лоцилиндрических поверхностей скольжения дает в ряде случаев несколько завышенный запас, а главное – в нем не учитываются усилия, действующие на вертикальные грани отсеков, что делает весь расчет приближенным и вызывает необходимость принятия дополнительных допущений.

Некоторые усовершенствования и упрощения расчетов по методу круглоцилиндрических поверхностей скольжения (введение переменности масштаба, но в прежней постановке задачи) внесены проф. Г. И. Тер-Степаняном и проф. М. Н. Гольдштейном, причем коэффициент устойчивости рекомендуется определять по выражению

где А и В — коэффициенты, зависящие от геометрических размеров сползающего клина, выраженные в долях от высоты откоса h; значения этих коэффициентов по вычислениям М. Н. Гольдштейна, приведены в таблицах.

Из выражения (4.16)

По формулам (4.16) и (4.16′) и данным таблиц легко вычисляют значения коэффициента устойчивости откоса η и предельную высоту откоса h при принятом коэффициенте устойчивости.

Для грунтов связных с незначительным углом внутреннего трения (при φ

Дата добавления: 2015-01-29 ; просмотров: 699 ; Нарушение авторских прав

Вопрос 7 – Метод кругло цилиндрических поверхностей скольжения

Основным недостатком рассмотренных выше методов является то, что полученные решения справедливы при относительно однородных пол физико-механическим свойствам массивах грунтов. В случае искусственно образованных откосов (откосы земляного полотна насыпей автомобильных дорог, плотин, дамб и т.п.) такая ситуация встречается достаточно часто. Однако при оценке устойчивости откосов глубоких выемок и природных склонов необходимо учитывать неоднородность грунтовых массивов. По инженерно-геологическим условиям потенциальные поверхности скольжения в массиве могут быть выраженными (прослои, оползневые смещения и т.д.) и не совпадать с предсказываемыми теорией предельного равновесия.

На практике чаще используют приближенные инженерные методы расчета.

К ним относят: метод кругло цилиндрических поверхностей скольжения, метод Шахунянца и др.

Метод кругло цилиндрических поверхностей скольжения впервые предложен К. Петерсоном в 1916 г. Метод называли «методом шведского геотехнического общества». В настоящее время имеются его различные модификации.

Потеря устойчивости откоса или склона, представленного на рисунке 26,а, может произойти в результате вращения отсека грунтового массива относительно некоторого центра О. Поверхность скольжения в этом случае будет представлена дугой окружности с радиусом r и центром в точке О. смещающийся массив рассматривают как недеформируемый (отвердевший) отсек, все точки которого участвуют в общем смещении. Коэффициент устойчивости определяют по формуле (7.19):

где М_sr и М_sa — моменты относительно центра вращения о всех сил, соответственно удерживающих и смещающих отсек.

Для определения входящих в формулу (7.19) моментов отсек грунтового массива разбивают вертикальными линиями на отдельные элементы. Характер разбивки назначают с учетом неоднородности грунта отсека и профиля склона так, чтобы в пределах основания каждого элемента прочностные характеристики φ и с были постоянными.

Вычисляют вертикальные силы, действующие на каждый элемент: собственный вес грунта в объеме элемента Р_giи равнодействующая нагрузки на его поверхности Р_qi. При необходимости могут быть учтены и другие воздействия (фильтрационные, сейсмические силы). Рассмотрим принципы их учета.

Равнодействующая сил Р_gi + Р_qi считается приложенной к основанию элемента и раскладывается на нормальную N_iи касательную T_iсоставляющие к участку дуги скольжения в точке их приложения.

Момент сил, вращающих отсек вокруг точки О, определится по выражению (7.21): n n

где n — число элементов в отсеке.

Принимают, что удерживающие силы T ‘_i в пределах основания каждого элемента обусловливаются сопротивлением сдвигу за счет внутреннего трения и сцепления грунта. Тогда с учетом выражения (5.2) можно записать (7.22):

где l_i — длина дуги основания i-го элемента, определяемая по формуле:

b_i — ширина элемента.

Отсюда, выражение для определения момента сил, удерживающих отсек, будет иметь вид (7.24):

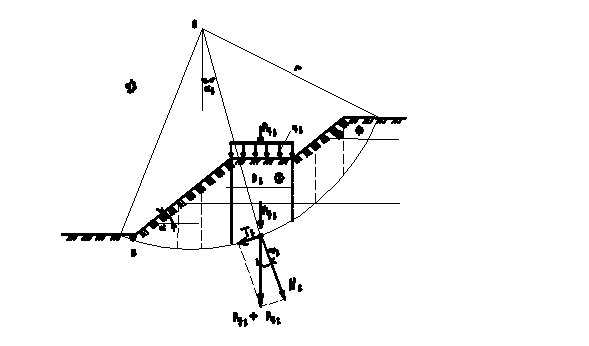
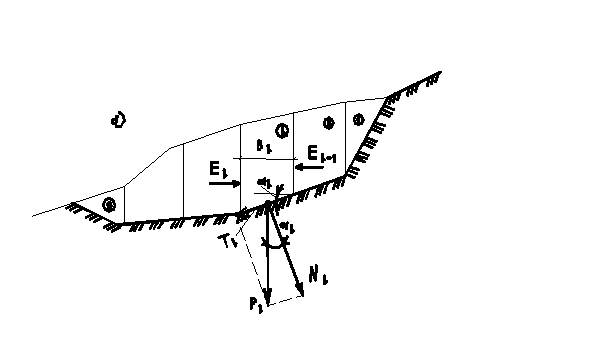
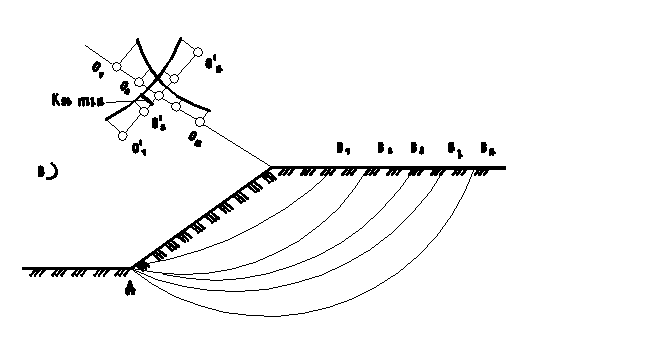
Рисунок 26 — Схема к расчету устойчивости откосов

методом кругло цилиндрических поверхностей скольжения:

1, 2, i … – номера элементов

Учитывая формулу (7.19), окончательно получим (7.25):

При k _st ≥ k н _st устойчивость отсека массива грунта относительно выбранного центра вращения О считается обеспеченной.

Сложность при практических расчетах заключается в том, что положение наиболее опасной поверхности скольжения неизвестно (неизвестно положение центра вращения и радиус дуги). Поэтому обычно проводится серия подобных расчетов при различных положениях центров вращения Ои значениях r. Чаще всего наиболее опасная поверхность скольжения проходит в районе нижней точки (подошвы) откоса или склона.

Один из приемов определения положения наиболее опасной поверхности скольжения заключается в следующем. Задаваясь координатами центров вращения О₁ , О ₂ , … , О _nна некоторой прямой положения центров вращения, определяют коэффициенты устойчивости k _{st , i} для соответствующих поверхностей скольжения и строят эпюру значений этих коэффициентов (Рисунок 26, в). Через точку О_min , соответствующую минимальному коэффициенту устойчивости, проводят по нормали второй отрезок и, располагая на нем новые центры вращенияО’₁ , О’₂ , … , О’_n , определяют коэффициенты устойчивости

k _{st , i} , для соответствующих поверхностей скольжения и строят эпюру этих коэффициентов (Рисунок 26, в). По этой эпюре вновь оценивают минимальное значение коэффициента устойчивости k _{st min}. Полученное значение k _{st min} и является мерой оценки устойчивости откоса или склона. Соответствующая этому значению коэффициента устойчивости кругло цилиндрическая поверхность скольжения рассматривается как наиболее опасная. Приведенная выше технология поиска наиболее опасной поверхности скольжения скорее соответствует технике «ручного» счета. В современных компьютерных программах при поиске наиболее вероятных поверхностей скольжения, как правило, назначается областьвозможных центров вращения с вариациями радиусов дуги скольжения. При k _{st min} ≥ k н _st устойчивость откоса и склона, согласно проектному заданию, считается обеспеченной.

Выполнение указанных расчетов «вручную» весьма трудоемко, поэтому разработаны многочисленные компьютерные программы с соответствующим сервисным обеспечением, позволяющие с минимальными затратами времени по вводу исходных данных получить обширную информацию об устойчивости откосов и склонов в количественных параметрах и графической интерпретации.

Устойчивость откосов связанных и сыпучих грунтов. Метод круглоцилиндрических поверхностей при исследовании устойчивости откосов.

Устойчивость откосов должна быть обеспечена при;

1. при откопке котлованов и траншей и т.п.

2. при строительстве зданий на бровке откосов

3. при проектировании земляных сооружений (насыпи, дамбы, грунтовые платины и т.п.

4. при оценке устойчивости естественных откосов

Виды оползней и разрушений: 1. скольжения, 2 вращения, 3. разжижения.

Существуют аналитический и графический методы расчёта

Аналитический наиболее простые решения были получены для идеально сыпучих и связанных грунтов.

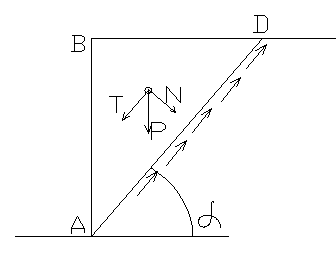
Идеально сыпучие грунты.(с=0, φ≠0 )

T’- сила трения T’=N*f где f- коэф. Трения

Из условия равновесия

P sinα – f P cosα = 0 откуда f= tg φ

Идеально связанные грунты (с≠0, φ=0)

допущения; — обрушение откоса по некоторой линии АD “c”- удельное сцепление

определяем вес призмы

P=((a*b)*(b*d)*γ)/2) * h = (h 2 *γ*ctgα)/2

(γ*h 2 *ctgφ*sinα)/2- (c/2)*(h/sinα) = 0

Метод круглоцилендрических поверхностей

Этот метод применяется для любых грунтов с введением допущений;

Основан на опытных данных о форме поверхности скольжения одной части грунта относительно другой

-Поверхность скольжения при обрушении круглоцилиндрическая;

-Отдельные блоки не оказывают давления друг на друга

Разбиваем на ряд отсеков и определяем для каждого вес ‘’P’’ и силу удельного сцепления ,,с,,

Силу Р раскладываем на состовляющие

Устойчивость откоса оценивается соотношением моментов удерживающих сил к моменту сдвигающих сил (относительно точки ,,О,,)

η – коэф устойчивости откоса и откос устойчив если η≥1,1….1,5

Для определения наиболее опасного положения поверхности скольжения

(координаты точки О )нужно ; провести из точки В лини ю под углом 36 0 Далее рассматриваем положение точек О1….Оn по этой линии. Определяем значения η и на перпендикулярах к линии ОВ стрем эпюру. По экстремуму эпюры определяем опасное положение точки О.

Определение давления сыпучих и связных грунтов на ограждения.

Данная задача ставится в следующих случаях;

1. при расчёте заглубленных сооружений на боковое давление грунта

2. при расчёте подпорных стен

3. при расчёте давления на конструкции от сыпучих материалов

Существуют аналитический и графоаналитический методы расчёта.

Аналитический наиболее простые решения получены для идеально сыпучих грунтов и однородных связанных грунтов.

Активное давление Еа действует в направлении смещения подпорной стены.

Ер- пассивное давление старается удержать подпорную стену от смещения.

Еа и Ер – определяются в предельнонапряжённом состоянии грунта.

Идеально-сыпучий грунт

Рассмотрим элементарный объём V на глубине z

γ – удельный вес грунта

на основании теории прочности Мора-Куллона

σ3=σ1*tg 2 (45 0 -φ/2)

Для определения активного и пассивного давления нужно найти равнодействующую.

tg 2 (45±(φ/2)) – обозначим ч-з α_а; α_р – коэф. Активного и пассивного давления

Ea= (γ*H 2 *tg 2 α_а)/2 Eр= (γ*H 2 *tg 2 α_р)/2

Однородно-связанные грунты

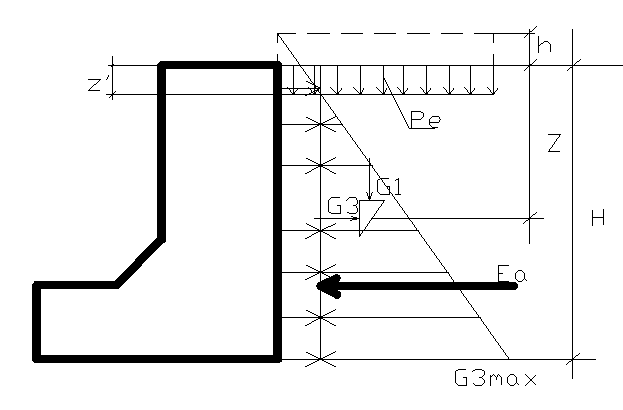
z’- расстояние от края подпорной стены до пересечения эпюр

Заменяем Ре на действие грунта высотой h и γ

σ3=γ(h+z)tg 2 (45-φ/2)-Pe

σ3=γztg 2 (45-φ/2) — 2c*tg(45-φ/2)

σ_φ3— характеризует давление без учёта удельного сцепления

σ_c3— показывает на сколько на сколько снижается давление при учёте сил сцепления z’ = 2c / (γ*tg(45-φ/2))

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Метод круглоцилиндрических поверхностей скольжения

Рассмотрим призму скольжения

Центром вращения «О» и соответственно величиной радиуса R задаются.

Призму скольжения разбивают вертикальными сечениями на ряд отсеков и принимают вес каждого отсека Р_i условно приложенным к точке пересечения линии действия веса с соответствующим отрезком дуги скольжения (рис.а). Силы веса раскладывают на направление радиуса вращения (N_i) и ему перпендикулярное (Т_i). Затем составляют уравнение равновесия в виде суммы моментов всех сил относительно центра вращения:

где: L – длина дуги скольжения АС,

φ – угол внутреннего трения грунта,

с – сцепление грунта,

Т_i=Р_isinφ – сила трения.

В этом уравнении первое слагаемое представляет собою сдвигающий момент, а два других – величину удерживающего момента противоположного направления:

Их отношение составляет коэффициент устойчивости откоса:

В этом выражении величина радиуса вращения R сократилась, а tgφ=f – коэффициент трения грунта по грунту.

Теперь требуется определить какая же кривая скольжения и какая величина коэффициента устойчивости откоса являются истинными? Этот вопрос решается путем последовательных попыток, задаваясь каждый раз различными кривыми скольжения (рис.б) до тех пор, пока не будет найдено такого положения, при котором коэффициент устойчивости имеет минимальное значение («критическая кривая»). Возможно и графическое определение положения центра критической кривой скольжения. Его предложил шведский исследователь Феллениус. С этой целью сначала находят положение центра критической кривой для грунта, не обладающего внутренним трением (φ=0) в зависимости от крутизны откоса:

Тогда таблица углов:

По Феллениусу, центр критической кривой лежит на продолжении прямой ОК, где «О» — центр кривой скольжения для случая φ=0, а «К» — точка на глубине h от подошвы откоса и вправо от нее на расстоянии 4,5h по горизонтальному направлению, где h – высота откосов.

Такое построение справедливо для случая однородного грунта, постоянной крутизны откоса и горизонтальной верхней поверхности. Также следует иметь в виду, что построение Феллениуса не является точным решением вопроса, оно указывает примерную зону расположения центра критической кривой скольжения и нуждается в дальнейшем уточнении путем нескольких дополнительных попыток.