Расчет устойчивости откосов метод маслова

Применение верификационных тестов при расчетах устойчивости земляного полотна железнодорожного пути

Анализ современного состояния проектирования, строительства и эксплуатации инфраструктурных объектов свидетельствует о необходимости реализации комплекса мер по повышению качества расчетных обоснований проектных решений. В настоящее время производить расчеты инфраструктурных объектов невозможны без применения современного программного обеспечения.

Для приведения уровня качества расчетных обоснований проектных решений современных инфраструктурных объектов строительства проектным организациям рекомендуется осуществлять расчеты не менее, чем по двум сертифицированным программных комплексов, проводить сопоставительный анализ полученных результатов, так называемая верификация. Такая практика широко применяется в развитых странах. Эти верификационные тесты предназначены для проверки инженером правильности расчета устойчивости земляного полотна железнодорожного пути в расчетной программе.

Органами государственной экспертизы рекомендуется запрашивать в необходимых случаях расчетные обоснования конструктивных решений с использованием двух независимо разработанных программ.

Как известно, земляное полотно железных дорог представляет собой сложный комплекс грунтовых объектов, работающих в сложных условиях природно-климатической среды и динамических нагрузок. Все элементы железнодорожного пути по прочности, устойчивости и состоянию должны обеспечивать безопасное движение поездов. Для проверки обеспечения безопасности состояния земляного полотна применяют различные расчеты.

Несмотря на большое многообразие методик и возможностей решения расчетов устойчивости земляного полотна, необходимо проводить оценку достоверности выполненных расчетов в различных геотехнических программах.

Положительным результатом верификации является соответствие результатов расчетов значениям «эталонного решения» с допустимой погрешностью. Погрешность определяется путем сравнения результатов расчета с «эталонными» решениями.

На основании общедоступных методик и примеров, приведенных в открытых литературных источниках, сотрудники института провели верификационный анализ в геотехнической программе GEO5 — Устойчивость откосов (Версия программы: 2016.49).

Верификационный тест № 1
Модель, описанная в [1-2], представляет собой простой анализ однородного склона с одинаковыми свойствами грунта. Эта модель впервые опубликована в исследовании [3]. Физико-механические свойства грунта склона: с = 3,0 kN/m2; φ = 19,6°; γ = 20,0 kN/m3.

Результаты расчета полученными различными методами приведены в таблице 1. Как видно из таблицы 1, результаты, полученные программами Slide, SVSLOPE и GEO5-Устойчивость откосов, достаточно хорошо согласуется. Отличия по полученным коэффициентам устойчивости составляет по методу Bishop и Spenser 0,2%.

Таблица 1 – Результаты верификационного анализа

Левая точка поверхности скольжения

Правая точка поверхности скольжения

«GEO5 — Устойчивость откосов»

Шахунянц

Верификационный тест № 2
Модель, описанная в [4], представляет собой простой анализ однородного склона сложенного из супеси, с одинаковыми свойствами грунта, с учетом уровня грунтовых вод. Дополнительно были проведены расчеты с укреплением анкерами. Физико-механические свойства грунта склона и характеристики анкера: с = 21,0 kN/m2; φ = 27,0°; γ = 18,5 kN/m3, γsat = 19,50 kN/m3, F = 20 kN/m2, FА = 200 kN, bA=2.00 м, Hзакрепления анкера = [x,z] = [16.00;9.00].
Результаты расчета, полученные различными методами, приведены в таблице 2. Как видно из таблицы 2, результаты расчета без оптимизации линии поверхности скольжения, полученные авторами и выполненные нами, совпадают. Нами также были дополнительно проведены расчеты с учетом оптимизации поверхности скольжения. Результат расчета с учетом оптимизацией на 1-4% меньше, чем без оптимизации. Что также необходимо учитывать при проектировании.

Таблица 2 – Результаты верификационного анализа

[4] и «GEO5 — Устойчивость откосов» (ООО «ИПИТ»)

Bishop (Anchored slope)

Spencer (Anchored slope)

Шахунянц

«GEO5 — Устойчивость откосов» с учетом оптимизации

Bishop(Anchored slope) (рис. 1)

Spencer (Anchored slope) (рис. 2)

Шахунянц

Шахунянц (Anchored slope) (рис. 3)

В строительной практике для определения устойчивости грунтового сооружения, как правило, используются методы предельного равновесия, регламентированные нормативными источниками и разработанные такими авторами как Шахунянц, Маслов, Терцаги, Бишоп, Моргенштерн, Спенсер и многими другими, однако ни один из авторов расчета устойчивости не предполагал в своем методе наличие геосинтетических прослоек. Отечественной нормативной документацией предлагаются методы учета геосинтетических материалов в расчетах, в то же время методы разнятся в зависимости от отрасли (а.д. или ж.д.), года выпуска и взглядов авторов документа. Единый подход для учета геосинтетических материалов в расчетах, регламентированный нормативной документацией, на данный момент отсутствует, в связи с чем, все чаще прибегают к расчетам методом численного моделирования.

Метод численного моделирования (программный комплекс Plaxis) позволяет решать сложные геотехнические задачи, связанные с индивидуальным проектированием и более корректно выполнять расчеты сооружений с геосинтетическими материалами, учитывая как прочностные характеристики материала, так и его деформацию в процессе эксплуатации (перемещение, растяжение, разрыв). В мировой практике применение подобных комплексов считается современным и актуальным подходом. Применение численных методов расчета с 2010 года начинает регламентироваться некоторыми отечественными нормативными источниками.

Вывод. Следует иметь в виду, что опыт накопленный в геотехническом проектировании свидетельствует о необходимости тщательного анализа и проверки полученных результатов. Также необходимо учитывать, что на рабочих компьютерах инженеров должны быть не один, а как минимум два программных расчетных комплексов.

Список использованных источников
[1] Rocscience Inc. (2015). Slope Stability. Verification Manual Part I. Slide. 2D limit equilibrium slope stability for soil and rock slopes Точка доступа: https://www.rocscience.com/help/slide/webhelp/pdf_files/verification/Slide_SlopeStabilityVerification_Part1.pdf (Дата обращения: 22.09.2016).
[2] SVSLOPE Slope Stability Modeling Software. Verification Manual SoilVision Systems Ltd. Saskatoon, Saskatchewan, Canada. Точка доступа: https://www.soilvision.com/downloads/software/svoffice2009/SVSlope_Verification_Manual.pdf (Дата обращения: 22.09.2016).
[3] Giam, P.S.K. and I.B. Donald (1989), «Example problems for testing soil slope stability programs», Civil Engineering Research Report No. 8/1989, Monash University, ISBN 0867469218, ISSN 01556282.
[4] GEO5 Slope Stability — Verfication manual. Точка доступа: http://www.finesoftware.ru/rukovodstvo-po-proverke/ (Дата обращения: 22.09.2016).

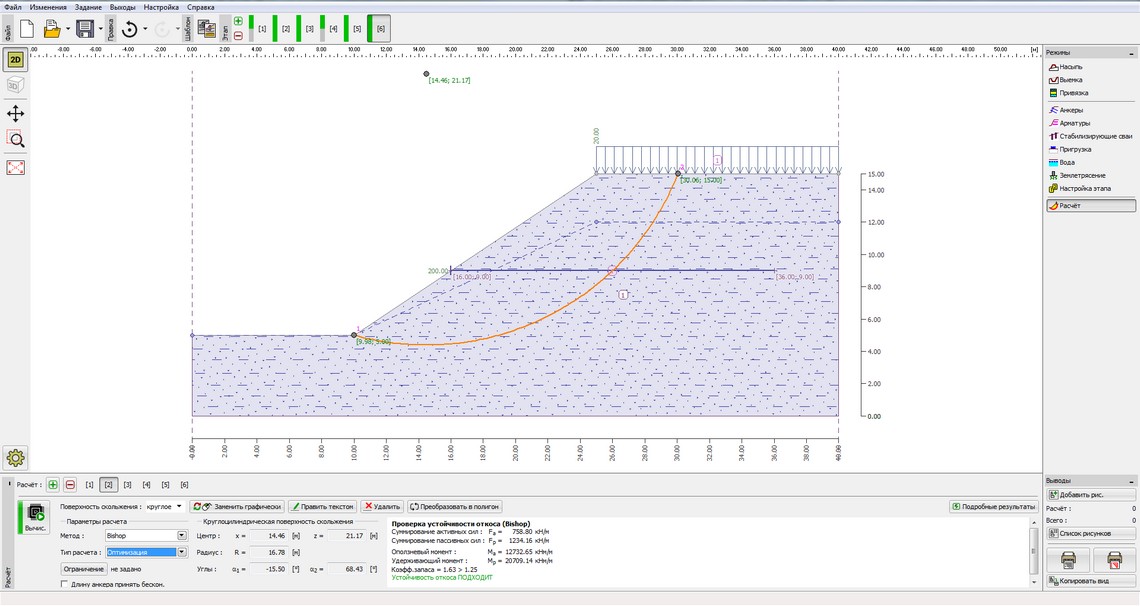
Рисунок 1 – Результаты расчета устойчивости откосов земляного полотна методом Bishop (Anchored slope) с оптимизированной поверхностью скольжения

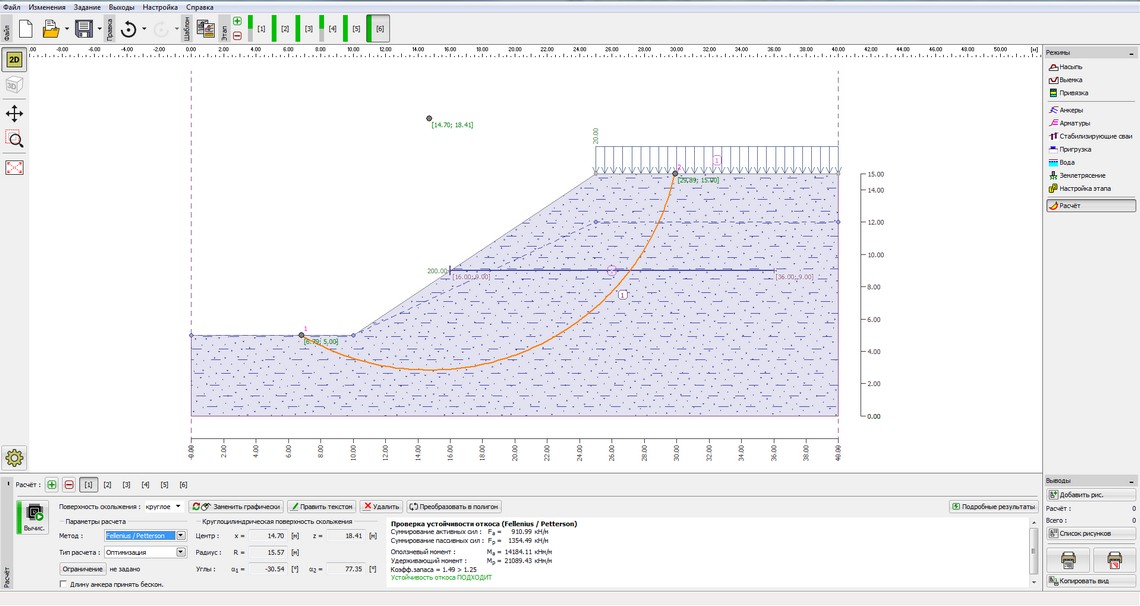
Рисунок 2 – Результаты расчета устойчивости откосов земляного полотна методом Fellenius/Petterson (Anchored slope) с оптимизированной поверхностью скольжения

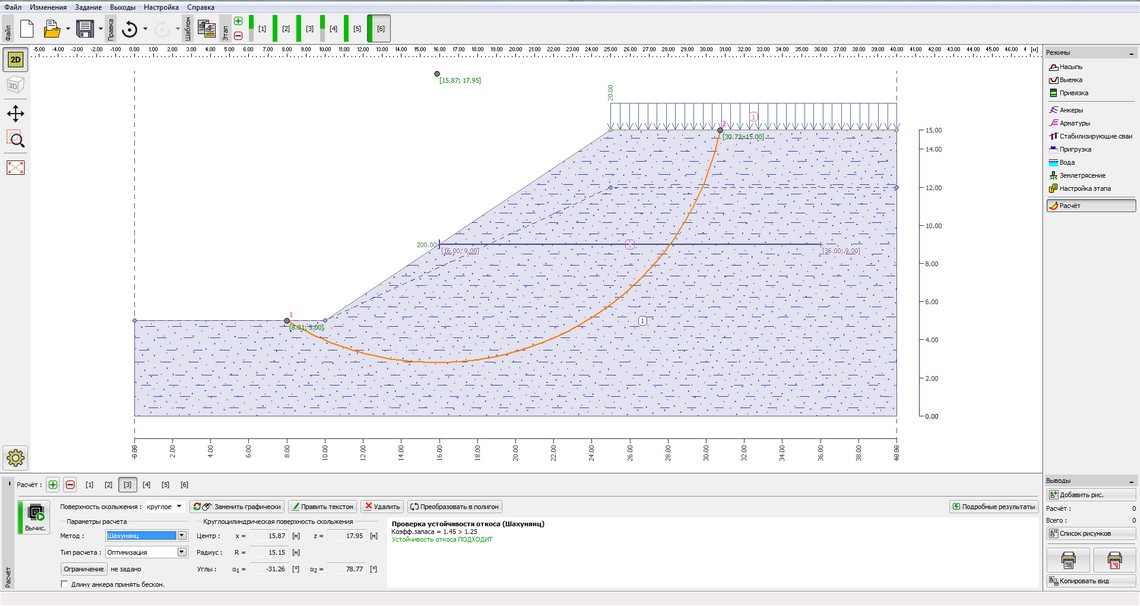
Рисунок 3 – Результаты расчета устойчивости откосов земляного полотна методом Шахунянц (Anchored slope) с оптимизированной поверхностью скольжения

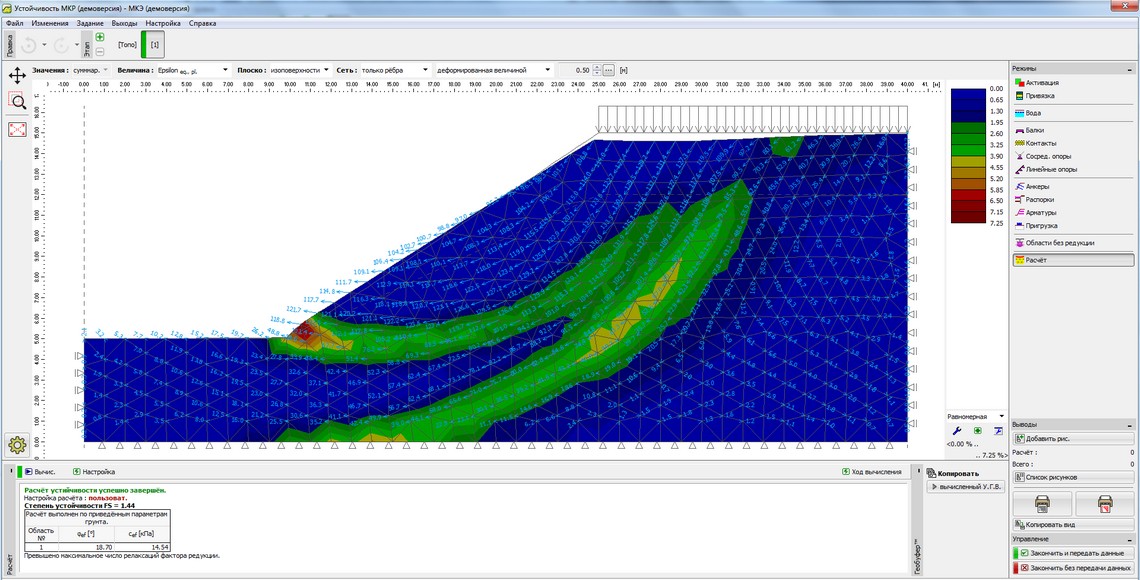
Рисунок 4 – Результаты расчета устойчивости откосов земляного полотна методом конечных элементов с выводом величины Epsilon

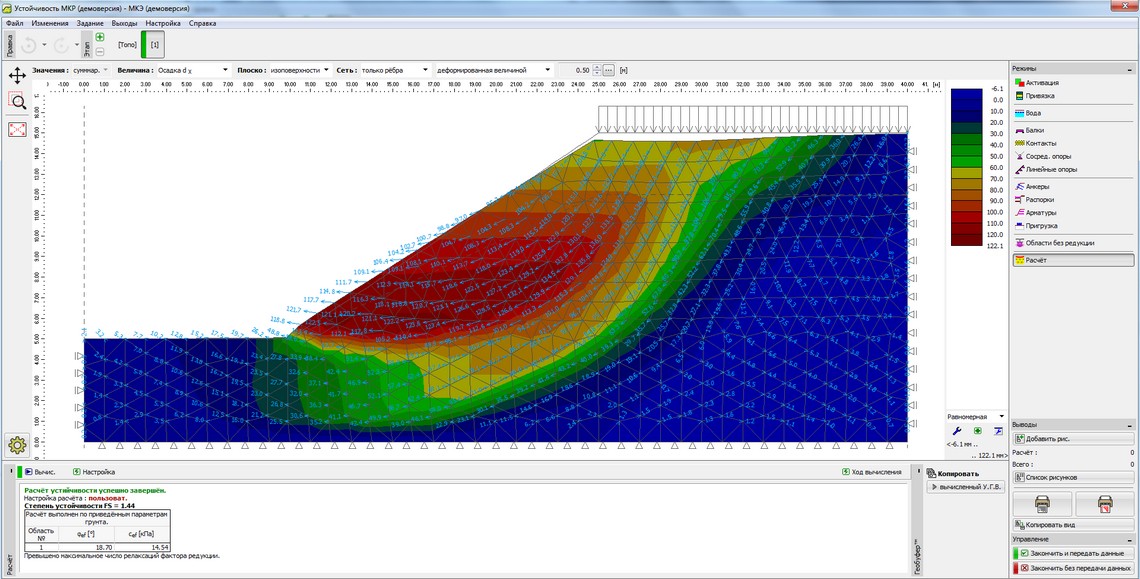
Рисунок 5 – Результаты расчета устойчивости откосов земляного полотна методом конечных элементов с выводом величины осадки dx

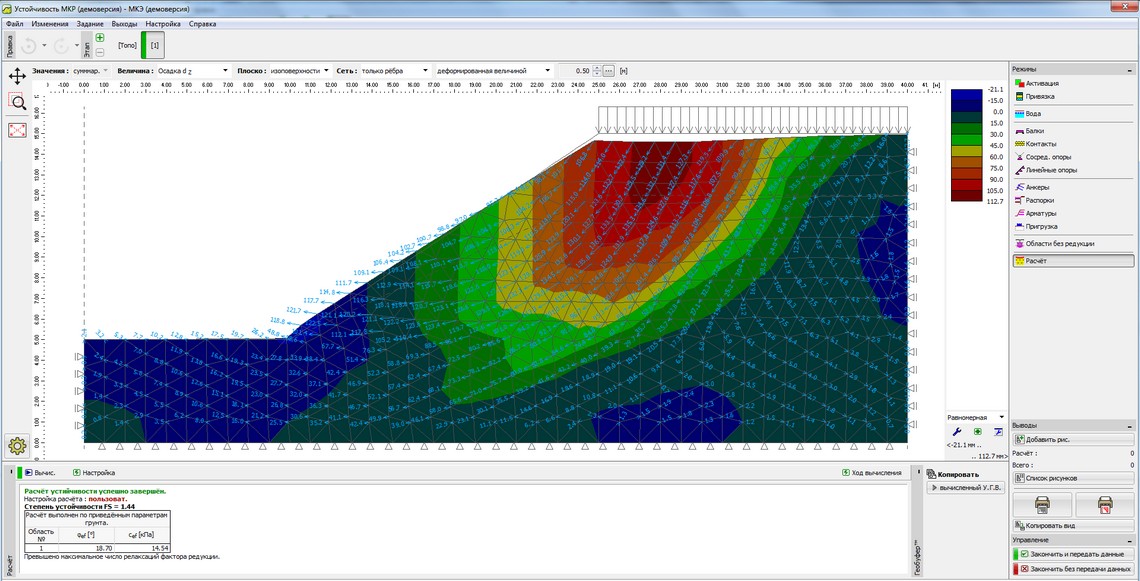
Рисунок 6 – Результаты расчета устойчивости откосов земляного полотна методом конечных элементов с выводом величины осадки dz

Механика грунтов. Физические свойства грунтов. Общие сведения о показателях физических свойств. Примеры решения задач по оценке классификационных показателей грунтов , страница 56

Последовательность построение очертания равноустойчивого откоса:

— Определяются расчетные характеристики грунта: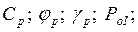

— Определяются условная глубина горизонтальной поверхности откоса:

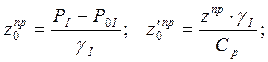
— В пределах заданной высоты откоса выделяются условный слой 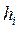, для которых определяются приведенная глубина заложения от условной поверхности:

;

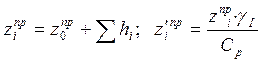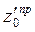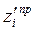— Для полученных и определяются горизонтальные координаты 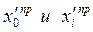точек на поверхности равноустойчивого откоса по рис. 13.4.

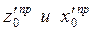— определяют верхнюю точку очертания откоса: х=0; у=0:

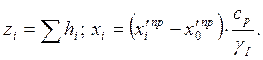
Полученные точки на поверхности равноустойчивого откоса соединяются хордами.

Приближенный метод построения очертания равнопрочного откоса в грунтах при с≠0 и φ≠0. (метод Маслова Н.Н.)

При оценке устойчивости откосов в условиях ппредельного напряженного состояния предлагается использовать показатели: угол сопротивления сдвигу 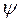и коэффициент сопротивления сдвигу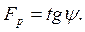

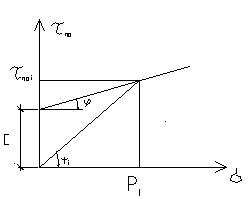
Рис. 13.5. Схема к определению коэффициента сдвига (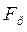) и угла сдвига в связных грунтах.

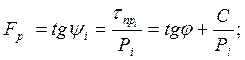
Из приведенной зависимости следует, что с увеличением напряжения (σ) в грунте коэффициент сдвига и угол сдвига уменьшаются.

При построении очертания равнопрочного откоса его высота условно разбивается на слои мощностью h_i. В уровне подошвы каждого выделенного слоя определяется напряжение 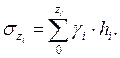При наличии нагрузки на поверхности грунта интенсивностью Р: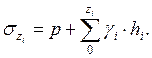

Для каждого условного слоя определяется очертание откоса в виде хорды с наклоном к горизонтальной поверхности:

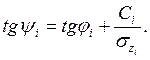
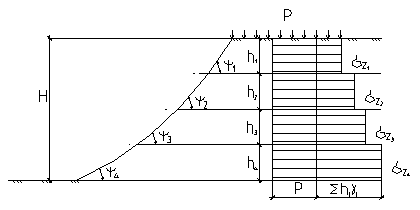
Рис. 13.6. Схема построения равнопрочного откоса по углу сдвига (ψ).

При слоистом напластовании грунтов по высоте откоса в каждом условно выделенном слое необходимо учитывать характеристики природных грунтов: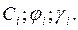

Расчет устойчивости откоса производится в разных условиях эксплуатации с различными показателями коэффициента устойчивости (к_st) при к_st=1,0 принимаются показатели грунта 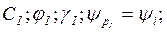при к_st>1,0 принимаются показатели грунта для I-ой группы предельных состояний,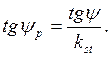

Метод круглоцилиндрических поверхностей скольжения для расчета устойчивости откосов.

Метод является наиболее распространенным из приближенных методов расчета устойчивости массивов грунта. Задача расчета заключается в определении коэффициента устойчивости, для наиболее опасной поверхности скольжения. Очертания поверхности скольжения принимают круглоцилиндрической на основании многочисленных наблюдений. Коэффициент устойчивости (к_st) определяется соотношением моментов удерживающих и сдвигающих сил относительно центра дуги скольжения. Сдвигающие силы обеспечиваются весом грунта. Удерживающие силы обеспечиваются внутренними сопротивлениями грунта сдвигам.

Для расчетов тело сползающего грунта условно делится вертикальными плоскостями на отдельные блоки объемом V_i и весом G_i. На дуге скольжения в i-ом блоке обеспечиваются нормальные силы 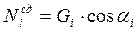и сдвигающие усилия 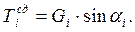Величина удерживающих сил: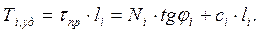

Сумма моментов удерживающих сил:

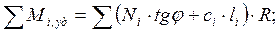
Сумма моментов сдвигающих сил:

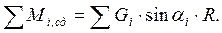
Величина коэффициента устойчивости определяется:

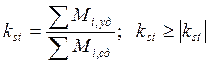
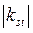— требуемая величина коэффициента устойчивости для проектируемого сооружения.

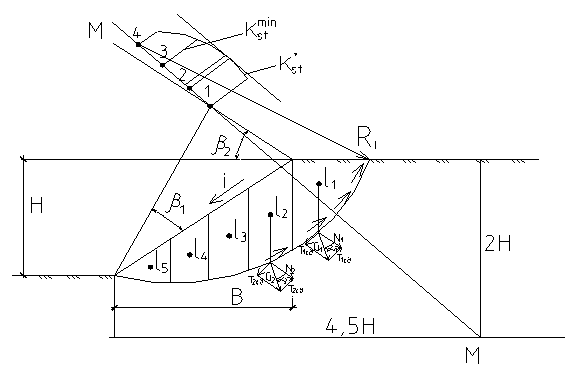
Рис. 13.7. Схема к расчету устойчивости откоса по методу круглоцилиндрических поверхностей скольжения.

Центр наиболее опасной поверхности скольжения лежит на оси М-М. Схема построения оси М-М приведена на рисунке 13.7. величины углов β₁ и β₂ принимаются по таблице 13.1. в зависимости от уклона откоса 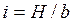. Расчет ведется по схеме последовательного приближения к .

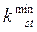Уклон откоса,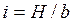

Расчет устойчивости откосов

Геотехническая постановка задачи

Расчет устойчивости откосов и склонов, противооползневых удерживающих инженерных сооружений, всегда основывается на данных инженерно-геологических и геотехнических изысканий, на количественном и качественном анализе оползневых факторов.

В настоящее время существует много методик по расчету устойчивости откосов, все они сводятся к трем базовым классам методов:

• методы предельного (пластического) равновесия;
• методы конечных элементов;
• комбинированные методы.

Выбор тех или иных методов в первую очередь определяется типом оползневого процесса и механизмом возможного смещения оползневых масс. Каждый оригинальный способ расчета характеризуется своей оригинальной системой, полученной в данном способе с использованием того или иного допущения (необходимость которого связана со статической неопределенностью задачи).

Класс методов предельного равновесия, может быть представлен методами Моргенштерна-Прайса, упрощенным методом Бишопа и обобщенным методом Янбу. Методы Бишопа и Моргенштерна-Прайса рассматриваются действующими нормативными документами (п. 4.2.11 СП 11-105-97, Часть II [4]) в качестве общепринятых методов расчета устойчивости склонов. Метод конечных элементов, представляющий класс численных методов и рекомендованный к применению в актуализированных редакциях нормативных документов (п. 5.2.3 СП 116.13330).

Метод Бишопа

При расчете устойчивости откосов, в упрощенном методе Бишопа удовлетворяются условия равновесия общих моментов и вертикальных сил (равновесие сдвигающих сил не соблюдается). Несмотря на то, что условия равновесия удовлетворяются не полностью, тем не менее, метод обеспечивает хорошие результаты и рекомендуется для проведения большинства практических расчетов, проводящихся по круглоцилиндрической поверхности. Многоугольник сил, построенный на основе метода Бишопа, показан на рисунке.

Вследствие того, что коэффициент устойчивости FS входит в обе части уравнения, для его решения необходимо задаться предположением о начальном значении коэффициента устойчивости. Далее решение данного уравнения сводится к итерационному процессу (до тех пор, пока вычисляемый FS не окажется меньше заданной допустимой погрешности).

Бишоп провел сопоставление коэффициентов запаса, полученных с помощью упрощенного и более строгих методов, которые удовлетворяют всем условиям равновесия. Он установил, что вертикальная составляющая сил взаимодействия может быть принята равной нулю, не приводя к существенным ошибкам, обычно с расхождением менее 5%. Следовательно, упрощенный подход, в котором вертикальные составляющие сил взаимодействия приводятся к нулю, обеспечивает тот же результат, что и строгий, при котором удовлетворяются все условия равновесия.

Метод Янбу

Метод Янбу был разработан в 1954 году норвежским профессором геотехники Нилмаром Оскаром Чарльзом Янбу. Он очень схож с методом Бишопа. С его помощью также, в геотехнической практике, выполняются расчеты оползневых склонов. Отличием является то, что в данном методе осуществляется удовлетворение равновесию сдвигающих сил, при этом не соблюдается удовлетворение равновесию моментов. Диаграмма распределения сил в отсеке и многоугольник сил, построенные при расчёте по упрощённому методу Янбу показаны на рисунке

Анализируя многоугольник сил в отсеке, можно сказать что многоугольник, получающийся по методу Янбу, замкнут лучше, чем в методе Бишопа. Стоит отметить, что при расчёте по круглоцилиндрической поверхности результаты по методу Янбу получаются заниженными.

Уравнение для вычисления коэффициента устойчивости по упрощённому методу Янбу показано на рисунке.

Упрощённый метод Янбу является наиболее близким к методу Маслова-Берера, рекомендованному российскими нормативными документами для расчёта устойчивости склонов, так как относится к группе методов горизонтальных сил, действующих на границе отсеков.

Метод конечных элементов

Метод конечных элементов (МКЭ, FEM) наряду с методами конечных разностей является одним из основных численных методов решения задач механики сплошной среды.

Одна из особенностей МКЭ состоит в том, что он базируется скорее на интегральной формулировке анализируемого явления, нежели на дифференциальной форме, которую представляют уравнения в частных производных и граничные условия. Эта интегральная формулировка может быть вариационного (если это возможно) либо проекционного типа.

Основная концепция метода конечных элементов состоит в том, что искомую непрерывную величину аппроксимируют кусочным набором простейших функций, заданных над ограниченными конечными подобластями (элементами). С помощью такой процедуры интегрирование дифференциальных уравнений аналитической постановки задачи сводится к решению системы линейных уравнений. Количественные значения неизвестной величины отыскиваются в ограниченном числе точек (узлов) области, а в пределах элементов значения неизвестной функции и ее производных определяются уже аппроксимирующими функциями и их производными.

Наиболее важными преимуществами МКЭ благодаря которым он так широко используется, являются:

• свойства материалов смежных элементов могут быть различными, что позволяет применять метод для моделирования напряженно-деформированного состояния неоднородных сред;
• методом можно пользоваться для областей с любой формой внешних и внутренних границ;
• размеры элементов могут быть переменными, что позволяет укрупнить или измельчить сеть разбиения области на элементы;
• с помощью МКЭ не представляет труда рассмотрение граничных условий с разрывной поверхностной нагрузкой, а также смешанных граничных условий.

Большое практическое применение МКЭ получил при решении геотехнических задач, касающихся расчета устойчивости откосов и склонов, так как позволяет учесть сложную геометрию откосов и их неоднородность.

В отличие от методов, основанных на анализе предельного равновесия, в МКЭ нахождение нормальных и касательных напряжений по поверхности скольжения осуществляется с учетом деформационных свойств грунтов (модуля Юнга и коэффициента Пуассона).

Анализ напряженного состояния методом конечных элементов удовлетворяет условиям статического равновесия и позволяет оценить изменения напряжений, вызванные варьированием деформационных свойств, неоднородности и геометрических форм.

Поле напряжений в откосе определяется решением двухмерной задачи плоской деформации с использованием конечных элементов треугольной формы. На рисунке выше показана конечно-элементная дискретизация, применяемая при расчетах откосов. Жесткие границы заданы на значительном расстоянии от откоса, поэтому наличие их не влияет на напряженное состояние откоса. В методе конечных элементов матрица жесткости элементов, которая связывает силы и перемещения в узлах, определяется исходя из минимизации полной потенциальной энергии. Эти матрицы жесткости затем накладываются, образуя общую матрицу жесткости системы. Задав силы и перемещения в каждом узле на границах, система совместных уравнений, базирующихся на общей матрице жесткости, может быть разрешена относительно перемещений каждого узла. После того как установлены перемещения, для каждого элемента можно определить напряжения.

Решение краевой задачи о напряженно-деформированном состоянии рассматриваемой расчетной области сводится к численному решению системы уравнений:[K] = , — вектор узловых перемещений; — вектор нагрузок.

При решении нелинейной задачи механики деформируемого твердого тела совместно с уравнением решается также другая система уравнений, задаваемая соотношением F(<�σ>, <�ε>) = 0.

При этом решение задачи сводится к подбору исходных параметров <�ε0>или <�σ0>(соответственно при использовании метода начальных деформаций или начальных напряжений), которые удовлетворяют условиям равновесия рассматриваемой расчетной области. Подбор этих параметров осуществляется итерационными методами.

Определение устойчивости склона выполняется методом редукции (ступенчатого уменьшения) прочностных параметров материалов модели, доводя модель до искусственного разрушения. Состояние математической модели, при котором не может быть получено устойчивое решение краевой задачи вследствие безграничного нарастания деформаций расчетной области, трактуется как предельное.

Коэффициент запаса несущей способности откосов и склонов определяется как отношение исходных прочностных параметров пород, слагающих рассматриваемый откос (склон) к их минимальным значениям, при которых решение краевой задачи еще возможно.

За рубежом, при моделировании устойчивости склонов, наиболее часто используется нижняя предельная теорема пластического разрушения.

В основе расчетных методов оценки устойчивости оползневых и оползнеопасных склонов лежат две предельные схемы (Р.Р. Чугаев, Ж. Косте, Г. Санглера).

Идея первой предельной схемы (фактических и уменьшенных прочностных характеристик) состоит в нахождении таких критических значений прочностных характеристик грунта, что бы расчетный склон перешел в состояние предельного равновесия. Соответственно коэффициент устойчивости при подобном подходе определяется как отношение фактических прочностных характеристик к их критическим значениям.

Идея второй предельной схемы (удерживающих и сдвигающих усилий) заключается в изучении соотношения сдвигающих и удерживающих усилий, действующих на склон. Коэффициент устойчивости в этом случае может быть определен как отношение удерживающих моментов к сдвигающим.

Стоит отметить, что определение коэффициента устойчивости в первом и во втором случае различно и использование первой предельной схемы с точки зрения механики более обосновано. Однако на практике оба определения коэффициента устойчивости дают близкие результаты.

Наша организация предлагает комплексный подход с целью оценки устойчивости склонов и откосов, а также разработке мероприятий по предупреждению развития и предотвращению активизации оползневого процесса. А также разработку документации для устройства инженерной защиты от оползней.

Более полную информацию по разработке геотехнического проекта инженерной защиты от оползней, по выполнению геотехнических расчетов вы можете получить позвонив нам по телефону + 7 (499) 350-23-58, или оставив заявку по форме или по электронной почте.

© 1999-2021 Научно-проектное конструкторское бюро «СтройПроект»

Метод расчета устойчивости путем снижения прочностных характеристик

Введение

В строительной практике для определения устойчивости грунтового сооружения или склона, как правило, используются методы предельного равновесия, разработанные такими авторами как Шахунянц, Маслов, Терцаги, Бишоп, Моргенштерн, Спенсер и многими другими.

В расчетной модели принимается ряд допущений [1]:

— используется гипотеза затвердевшего тела;

— допускается определенная форма поверхности скольжения;

— напряжения заменяются силами;

— принимаются допущения о давлении грунтовых вод и сейсмичности.

Общая последовательность применения методов предельного равновесия такова, что сначала задаются поверхностью скольжения, после чего путем итераций определяется положение критической поверхности скольжения с минимальным значением коэффициента устойчивости. Как следует из приведенной последовательности, недостатком этого подхода является то, что поверхность скольжения задается до начала расчета. Как правило, решение о возможной форме поверхности скольжения принимается на основе расчетов по круглоцилиндрическим, или по полигональным (предопределенным) поверхностям скольжения [2], однако существуют такие программы, в которых поверхность скольжения может быть комбинированной или задана логарифмической спиралью (GenID32, Slide).

Таким образом, исходя из необходимости охватить как можно больше встречающихся на практике случаев (разнородное геологическое строение, наличие грунтовых вод, сейсмические воздействия и пр.) методы предельного равновесия имеют много допущений и упрощений, но при этом позволяют получать достаточные для практики результаты в случае наличия инженерно-геологических условий средней степени сложности.

Сложности использования методов предельного равновесия

Существует большое количество программ, реализующих методы предельного равновесия (GGU Stability; GeoStab; GeoStudio; SlopeStability; Slide; DCGeotex; MRE; MacStars 2000, GenID32 и др.), призванных облегчить работу проектировщика-расчетчика. Проблемами использования программ является отсутствие доступной для проектировщика информации и применимости того или иного метода (как правило зарубежного), отсутствие в нормативных документах четкого указания на применение конкретного метода расчета и разница (в некоторых случаях существенная) между заложенными в программу методами расчета устойчивости.

Известный специалист по расчетам устойчивости в области гидротехнического строительства Р.Р. Чугаев, анализируя большое разнообразие методов расчета устойчивости, выделил всего четыре способа, отличающиеся своей оригинальной системой сил, действующих на отсеки (это связано с невозможностью рассчитать статически неопределимую систему, образованную рядом твердых отсеков-столбиков, стоящих на дуге обрушения, пользуясь только тремя уравнениями статики): Свена-Гультена, Феллениуса, Крея, Терцаги. Другие известные способы (Бишопа, Маслова, Шахунянца и др.) касаются главным образом только техники расчетов или учета тех или иных дополнительных усложняющих элементов, при этом такого рода предложения не затрагивают существо самих силовых схем, положенных в основу расчета [3].

Методы расчета делятся по механизмам: удовлетворяющие общему равновесию моментов (Феллениуса, Бишопа), методы равновесия сил (Шахунянца, Крея, Маслова-Берера) и методы равновесия моментов и сил (Янбу, Моргенштейна и Прайса, Спенсера).

Еще одним существенным различием методов расчета устойчивости является учет сил. Можно выделить три категории методов (рис. 1):

— учитывающие только основные силы;

— учитывающие горизонтальные силы взаимодействия отсеков;

— учитывающие вертикальные и горизонтальные силы взаимодействия между отсеками.

Рис. 1 Схемы учета сил: а) только основные; б) основные и горизонтальные;
в) основные, горизонтальные и вертикальные.

Если судить по критерию максимального учета сил, воздействующих на отсек, то такие методы как Н. Моргенштейна и В. Прайса, а также
Е. Спенсера являются наиболее достоверными.

Общая рекомендация по оценке результатов расчета такова: методы
Н. Моргенштейна, В. Прайса и Е. Спенсера, а также метод GLE (General Limit Equilibrium) дают наиболее точный результат, их следует сравнивать с коэффициентом запаса устойчивости; методы Г. М. Шахунянца, А. Бишопа, Н. Янбу считаются консервативными, следовательно, занижают устойчивость и могут применяться для проверки устойчивости относительно состояния предельного равновесия (Куст=1). Методы В. Феллениуса и ему подобные в современных мощных программах по расчету устойчивости добавлены только лишь потому, что многим пользователям они хорошо знакомы, но результаты имеют очень большое занижение устойчивости, а часто не являются корректными. Эта рекомендация действительна при полных и достоверных исходных данных! В любом случае все решает опыт и интуиция расчетчика.

По опыту использования различных программ можно сказать, что в случаях расчетов сложных оползневых склонов, чтобы выявить наихудшее положение линии поверхности скольжения, требуется выполнение расчетов по различным поверхностям скольжения и с заданием разного рода ограничений, что требует определенного навыка и опыта. А в случаях, казалось бы, более простых, как например армирование высокой насыпи, возникают сложности с определением окончательного коэффициента устойчивости, поскольку большая часть методов свидетельствует об устойчивом состоянии, а считающийся в нашей стране наиболее достоверным метод проф. Шахунянца показывает, что устойчивость недостаточна.

Здесь следует понимать, что ни один из авторов методов расчета устойчивости не предполагал в своем методе наличие геосинтетических прослоек [4,5].

Метод снижения прочности

Способом определения устойчивости, лишенным описанных недостатков, является метод снижения прочности. Во-первых, согласно положенному в основу принципу, поверхность скольжения определяется автоматически в ходе расчета, а во-вторых, учет геосинтетических прослоек в программах, использующих этот метод, на наш взгляд более совершенен [4,5].

Из положений механики грунтов известно, что напряженное состояние в какой-либо точке грунта рассматривается как предельное в том случае, когда незначительное добавочное воздействие нарушает равновесие и приводит грунт в неустойчивое состояние. Разрушение грунта происходит в результате преодоления внутренних сил трения и сцепления между частицами по определенным поверхностям скольжения.

В общем виде устойчивость сооружения определяется коэффициентом безопасности, представляющим собой отношение максимально возможной прочности грунта τ_пред к минимальному значению, необходимому для обеспечения равновесия τ_действ:

(1)

Если формулу (1) представить в виде стандартного условия Кулона, то она примет вид:

Где с’ и j’ – исходные параметры прочности и s_n – фактическое нормальное напряжение; с_r и j_r – параметры прочности, сниженные в ходе расчета до минимальных значений, достаточных для поддержания равновесия.

Метод снижения прочности (SRM – shear reduction method) по принципу расчета схож с методом Р.Р. Чугаева, известным в гидротехническом строительстве [3]. Метод снижения прочности реализован в программах, работающих на основе метода конечных элементов и конечных разностей (Plaxis, GEO5, Phase2, FLAC). Прогноз разрушения осуществляется путем одновременного понижения обоих показателей сдвиговой прочности:

Где К_уст – коэффициент снижения прочности, соответствующий коэффициенту устойчивости в момент разрушения.

Последовательность расчета следующая: коэффициенту снижения прочности (К_уст) присваивается значение К_уст=1. В ходе расчета К_уст увеличивается, при этом сопротивление сдвигу и деформация оцениваются на каждом этапе до наступления разрушения. Результаты вычислений приводятся в виде графиков, на которых показано влияние коэффициента снижения прочности (К_уст) на смещение контрольной точки (узла сетки конечных элементов). Критерий разрушения модели определяется условием Кулона-Мора. Если в результате конечно-элементного расчета будет получено решение для последнего устойчивого состояния откоса, то график расчетов примет горизонтальное положение и коэффициент снижения прочности будет соответствовать коэффициенту устойчивости К_уст. Поверхность скольжения при использовании МКЭ формируется во время расчета.

Существенным преимуществом метода снижения прочности по сравнению с методами предельного равновесия является то, что поверхность скольжения и коэффициент устойчивости определяются одновременно в процессе расчета.

Применение численных методов расчета (МКЭ) регламентируется такими документами, как: СП 16.13330.2012 «Инженерная защита территорий, зданий и сооружений от опасных геологических процессов. Основные положения» (Актуализированная редакция СНиП 22-02-2003) и ОДМ 218.2.006-2010 Рекомендации по расчету устойчивости оползнеопасных склонов (откосов) и определению оползневых давлений на инженерные сооружения автомобильных дорог. ОДМ 218.001-2009 «Рекомендации по проектированию и строительству водопропускных сооружений из металлических гофрированных структур на автомобильных дорогах общего пользования с учетом региональных условий (дорожно-климатических зон)».

Проведенные анализы сопоставления расчетов устойчивости по методам предельного равновесия и снижения прочности для большого количества параметров насыпей с различной конфигурацией показали, что такие методы, как Тейлора (с расчетом по недренированной прочности c_u), Бишопа, Моргенштейна (прочность задалась эффективными характеристиками с’ и φ’), которые можно считать проверенными временем, не имеют большого расхождения с расчетами по методу снижения прочности. Расхождения в несколько процентов связаны с тем, что МПР используют исключительно круглоцилиндрические поверхности скольжения, а метод снижения прочности не имеет никаких ограничений по геометрии механизма разрушения [2].

Еще одним существенным преимуществом использования метода снижения прочности является его единство с другими возможностями численного моделирования. Это обстоятельство позволяет принять в расчет погруженную часть насыпи при расчете устойчивости на слабых (сжимаемых) грунтах, с учетом процессов консолидации основания и его упрочнения, чего никаким образом нельзя сделать при расчете методами предельного равновесия. А также выполнять расчет устойчивости с учетом избыточного порового давления, формирующего «отпор» в центральной части насыпи и способствующего снижению устойчивости откосных частей, где эффективные давления максимальные (рис. 2). При таком расчете устойчивость насыпей на водонасыщенных глинистых грунтах оказывается значительно ниже.

Рис. 2 Схема к расчету устойчивости с учетом избыточного порового давления

Использование численного моделирования и расчет устойчивости по методу снижения прочности позволяет решать задачу по определению длительной прочности геосинтетических материалов. При расчетах по МПР (упруго-пластический расчет) необходимо задаться длительной прочностью R мпр _длит (рис. 3), определяемой по [6,7], и произвести оценку устойчивости, после чего будет известна кратковременная (номинальная) прочность R мпр _кр. При численном моделировании (консолидационный расчет) с учетом «отпора» сил избыточного порового давления для обеспечения устойчивости сооружения потребуется расчетная длительная прочность геоматериала R конс _длит> R мпр _длит, которая после завершения процесса консолидации снизится. Учитывая, что под длительной прочностью подразумевается остаточная прочность в расчете на 120 лет, в результате численного расчета получается, что кратковременная (номинальная) прочность, полученная с учетом процессов консолидации, меньше, чем полученная при расчетах методами предельного равновесия R конс _кр мпр _кр.

Рис. 3 График определения длительной прочности геосинтетического материала

Заключение

Использование численного моделирования позволяет решать сложные геотехнические задачи, связанные с индивидуальным проектированием, которые достаточно часто встают перед проектными организациями. Положенный в основу программ численного моделирования метод расчета устойчивости путем снижения прочностных характеристик имеет ряд преимуществ перед традиционно используемыми методами расчета устойчивости на основе уравнений предельного равновесия. Для простых случаев все методы дают одинаковый результат, однако термин «индивидуальное проектирование» подразумевает сложные инженерно-геологические условия, что требует применения более точных методов расчета.

Сложность освоения программ численного моделирования, отсутствие соответствующих предметов у студентов строительных вузов, а также ограниченное количество литературы по этому вопросу накладывает ограничения на использование этих методов. Однако в мировой практике использование геотехнических программных комплексов считается современным и актуальным. В то же время не стоит отказываться от традиционных методов предельного равновесия для проверки полученных результатов, поскольку численное моделирование ввиду сложности требует серьезного опыта и интуиции.

Библиографический список

1. Рекомендации по выбору методов расчета коэффициента устойчивости склона и оползневого давления М.:ЦБНТИ, 1986.

2. W.F. Van Impe, R.D. Verastegui Flores Underwater Embankments on Soft Soil: A Case History. University of Ghent, Belgium.

3. Чугаев Р.Р. Расчёт устойчивости земляных откосов и бетонных плотин на нескальном основании по методу круглоцилиндрических поверхностей обрушения. М.: Госэнергоиздат, 1963. — 144 с.

4. Вавринюк Т.С., Федоренко Е.В. Расчеты устойчивости земляного полотна с геосинтетическими материалами. Журнал «Красная линия», выпуск Дороги №69 май 2013.

5. Рекомендации по применению геосинтетических материалов в конструкциях промысловых дорог. СПб.:Миаком, 2013.

6. ОДМ 218.5.003-2010 Рекомендации по применению геосинтетических материалов при строительстве и ремонте автомобильных дорог.

7. Пособие по проектированию земляного полотна автомобильных дорог на слабых грунтах. М., 2004.

8. Геотехника и геосинтетика в вопросах и ответах. Справочное пособие. 2016

9. Практикум по Plaxis. Часть 1. Виртуальная лаборатория Soil Test. 2016 (электронное издание)

10. Практикум по Plaxis. Часть 2. Напряжения. Прочность/ 2016 (электронное издание)