Равноустойчивый откос по маслову
УСТОЙЧИВОСТЬ ОТКОСА, СЛОЖЕННОГО ГРУНТАМИ, ОБЛАДАЮЩИМИ ТРЕНИЕМ И СЦЕПЛЕНИЕМ
Для откосов, сложенных грунтами, обладающими трением и сцеплением, разработаны многочисленные методы расчетов как строгие, так и приближенные.
Одним из методов является решение В.В. Соколовского.
Решения В.В. Соколовского. На основе решение плоской задачи предельного равновесия В.В. Соколовский получил решение для определения очертания равноустойчивого откоса, сложенного из грунтов, обладающих трением и сцеплением. На рис. 6.5 приведены графики этого решения, которые представляют собой безразмерные координаты равноустойчивых откосов для различных углов внутреннего трения φ. Истинные координаты откосов будут равны:
 и  .
|
(6.3) |
Таким образом, безразмерные координаты х / и у / равноустойчивых откосов, указанные на графиках, уточняются внесением постоянной для данных грунтов поправки, равной отношению сцепления к объему веса грунта.
Рис. 6.5. Очертание равноустойчивых откосов
в безразмерных координатах
Из приближенных методов наиболее известен метод критического круга скольжения К. Терцаги, в котором допускается, что разрушение откоса произойдет по поверхности скольжения в виде дуги окружности, проходящей через подошву откоса, а также метод круглоцилиндрических поверхностей скольжения. Модификацией метода критического круга скольжения Терцаги, применяемого для оценки устойчивости откосов, является метод круглоцилиндрических поверхностей скольжения. Сущность его состоит в отыскании графоаналитическим способом такой круглоцилиндрической поверхности скольжения, проходящей через основание откоса, при которой коэффициент устойчивости грунта откоса будет минимальным (рис. 6.6).
При этом коэффициент устойчивости η будет равен:
 ,
|
(6.6) |
где 
— сумма нормальных сил, действующих радиально относительно поверхности скольжения;
— коэффициент трения;
с – удельная сила сцепления в пределах участка дуги поверхности скольжения;
l – длина дуги поверхности скольжения;
— сумма сдвигающих сил, действующих по касательным к поверхности скольжения.
Рис. 6.6. Определение устойчивости откоса по методу
круглоцилиндрических поверхностей скольжения.
При практическом использовании метода из некоего произвольного центра О1 радиусом R через точку а основания откоса проводят поверхность скольжения аб. Участок откоса, ограниченный дугой аб и ломанной линией откоса amb, разбивают на ряд призм, вес которых Q1, Q2, Q3, … , Qn… подсчитывают как площади соответствующих геометрических фигур, умноженные на удельный вес грунта γ. Силы, удерживающие N и сдвигающие Т, будут найдены соответственно:
 ;  .
|
(6.7) |
После определения η1 повторяют построения и расчеты при цилиндрических поверхностях скольжения, проведенных из новых центров О2, О3 и т.д., до тех пор, пока не будет найдено минимальное значение ηmin на первой вертикали. Аналогично находят минимальный коэффициент устойчивости ηmin для второй вертикали путем построения цилиндрических поверхностей скольжения из центров О4, О5, О6 и т.д., а затем для третьей и следующих вертикалей до тех пор, пока не будет найден минимум миниморум коэффициента устойчивости ηmin min. Цилиндрическая поверхность скольжения, соответствующая коэффициенту устойчивости ηmin min, является наиболее вероятной поверхностью скольжения грунтов склона. Устойчивость склона считается обеспеченной, если ηmin min > 1.
Определение коэффициента устойчивости ηmin min описанным выше способом связано с довольно громоздкими построениями и аналитическими подсчетами, поэтому рядом авторов выполнены решения этой задачи для некоторых часто встречающихся случаев.
М.Н. Гольдштейн предложил следующие формулы для определения коэффициента устойчивости откоса, соответствующего наиболее невыгодному очертанию цилиндрической поверхности скольжения и для определения критической высоты откоса при известных других параметрах:
 ,
|
(6.7) |
 ,
|
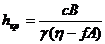(6.8) |
где 
— коэффициент трения грунта;
hкр – критическая высота устойчивости откоса;
А и В – коэффициенты, зависящие от угла заложения откоса и глубины прохождения поверхности скольжения, определяются по табл. 22П;
η – коэффициент устойчивости.
Существует ряд других методов оценки устойчивости откосов и склонов, например: широко описанный в литературе метод горизонтальных сил Берера-Маслова, метод равнопрочного откоса и др.
